Advertisements
Advertisements
प्रश्न
Prove that two different circles cannot intersect each other at more than two points.
उत्तर
Suppose two circles intersect in three points A,B,C,
Then A,B,C are non-collinear. So, a unique circle passes through these three points. This is contradiction to the face that two given circles are passing through A,B,C. Hence, two circles cannot intersect each other at more than two points.
APPEARS IN
संबंधित प्रश्न
In Fig. 1, QR is a common tangent to the given circles, touching externally at the point T. The tangent at T meets QR at P. If PT = 3.8 cm, then the length of QR (in cm) is :
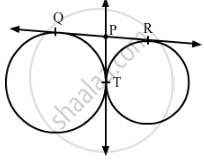
(A) 3.8
(B) 7.6
(C) 5.7
(D) 1.9
In fig., O is the centre of the circle, PA and PB are tangent segments. Show that the quadrilateral AOBP is cyclic.
Fill in the blank
The angle between tangent at a point on a circle and the radius through the point is ........
In a cyclic quadrilateral ABCD, if m ∠A = 3 (m ∠C). Find m ∠A.
In the given figure, chord EF || chord GH. Prove that, chord EG ≅ chord FH. Fill in the blanks and write the proof.

Find the radius of the circle
Diameter = 76 cm
If the angle between two radii of a circle is 130°, then the angle between the tangents at the ends of the radii is ______
In the following figure, tangents PQ and PR are drawn to a circle such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ, then ∠RQS.
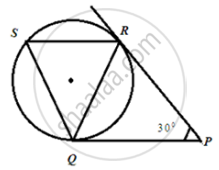
The length of the tangent from point A to a circle, of radius 3 cm, is 4 cm. The distance of A from the centre of the circle is ______
AB is a chord of a circle with centre O. AOC is diameter of circle, AT is a tangent at A.
Write answers of the following questions:
- Draw the figure using the given information.
- Find the measures of ∠CAT and ∠ABC with reasons.
- Whether ∠CAT and ∠ABC are congruent? Justify your answer.
