Advertisements
Advertisements
प्रश्न
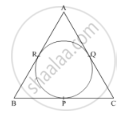
In Fig. 4, an isosceles triangle ABC, with AB = AC, circumscribes a circle. Prove that the point of contact P bisects the base BC.
उत्तर
Given: An isosceles ΔABC with AB = AC, circumscribing a circle.
To prove: P bisects BC
Proof: AR and AQ are the tangents drawn from an external point A to the circle.
∴ AR = AQ (Tangents drawn from an external point to the circle are equal)
Similarly, BR = BP and CP = CQ.
It is given that in ΔABC, AB = AC.
⇒ AR + RB = AQ + QC
⇒ BR = QC (As AR = AQ)
⇒ BP = CP (As BR = BP and CP = CQ)
⇒ P bisects BC
Hence, the result is proved.
APPEARS IN
संबंधित प्रश्न
In the given figure, O is the centre of the circle. PA and PB are tangents. Show that AOBP is cyclic quadrilateral.

In a cyclic quadrilateral ABCD if AB || CD and ∠B = 70°, find the remaining angles.
In the following figure, OABC is a square. A circle is drawn with O as centre which meets OC at P and OA at Q.
Prove that:
( i ) ΔOPA ≅ ΔOQC
( ii ) ΔBPC ≅ ΔBQA
Suppose you are given a circle. Describe a method by which you can find the center of this circle.
Draw a circle of diameter 7 cm. Draw two radii of this circle such that the angle between these radii is 90°. Shade the minor sector obtained. Write a special name for this sector.
Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord
A chord is at a distance of 15 cm from the centre of the circle of radius 25 cm. The length of the chord is
O is the circumcentre of the triangle ABC and D is the mid-point of the base BC. Prove that ∠BOD = ∠A.
Is every diameter of a circle also a chord?
Is every chord of a circle also a diameter?
