Advertisements
Advertisements
प्रश्न
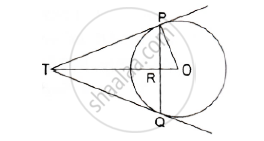
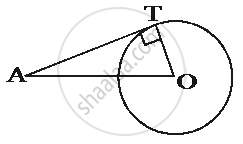
In the given figure, O is the centre of the circle. PA and PB are tangents. Show that AOBP is cyclic quadrilateral.

उत्तर
We know that the radius and tangent are perpendicular at their point of contact
∵ ∠OBP = ∠OAP = 90°
Now, In quadrilateral AOBP
∠APB +∠AOB + ∠OBP + ∠OAP = 360° [Angle sum property of a quadrilateral]
⇒ ∠APB + ∠AOB + 90° + 90° = 360°
⇒∠APB + ∠AOB =180°
Since, the sum of the opposite angles of the quadrilateral is 180°
Hence, AOBP is a cyclic quadrilateral
APPEARS IN
संबंधित प्रश्न
In the given figure, PQ is a chord of length 8cm of a circle of radius 5cm. The tangents at P and Q intersect at a point T. Find the length TP

Write True or False. Give reasons for your answers.
If a circle is divided into three equal arcs, each is a major arc.
PQ is a chord of length 4.8 cm of a circle of radius 3cm. The tangents at P and Q intersect at a point T as shown in the figure. Find the length of TP.
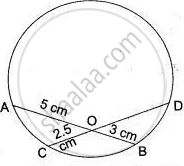
In Fig., chords AB and CD of the circle intersect at O. AO = 5 cm, BO = 3 cm and CO = 2.5 cm. Determine the length of DO.
Construct a triangle ABC with AB = 5 cm, ∠B = 60° and BC = 6. 4 cm. Draw the incircle of the triangle ABC.
Find the missing values in the following table for the circles with radius (r), diameter (d) and Circumference (C).
| radius (r) | diameter (d) | Circumference (C) |
| 15 cm |
A, B, C are any points on the circle with centre O. If m(arc BC) = 110° and m(arc AB) = 125°, find measure arc AC.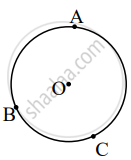
If the radii of two concentric circles are 4 cm and 5 cm, then the length of each chord of one circle which is tangent to the other circle is ______
A point A is 26 cm away from the centre of a circle and the length of the tangent drawn from A to the circle is 24 cm. Find the radius of the circle.
In the given figure, O is the centre of the circle. Shade sectors OAC and OPB.