Advertisements
Advertisements
प्रश्न
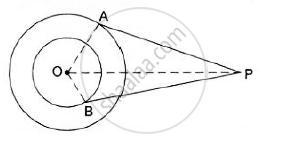
In the given figure, O is the centre of the circle. PA and PB are tangents. Show that AOBP is cyclic quadrilateral.

उत्तर
We know that the radius and tangent are perpendicular at their point of contact
∵ ∠OBP = ∠OAP = 90°
Now, In quadrilateral AOBP
∠APB +∠AOB + ∠OBP + ∠OAP = 360° [Angle sum property of a quadrilateral]
⇒ ∠APB + ∠AOB + 90° + 90° = 360°
⇒∠APB + ∠AOB =180°
Since, the sum of the opposite angles of the quadrilateral is 180°
Hence, AOBP is a cyclic quadrilateral
APPEARS IN
संबंधित प्रश्न
In two concentric circles, prove that all chords of the outer circle which touch the inner circle are of equal length.
In the given figure, O is the centre of the two concentric circles of radii 4 cm and 6cm respectively. AP and PB are tangents to the outer and inner circle respectively. If PA = 10cm, find the length of PB up to one place of the decimal.
In two concentric circles, a chord of length 8 cm of the large circle touches the smaller circle. If the radius of the larger circle is 5 cm, then find the radius of the smaller circle.
The circumference of a circle is 22 cm. The area of its quadrant (in cm2) is
A is a point at a distance 13 cm from the centre O of a circle of radius 5 cm. AP and AQ are the tangents to the circle at P and Q. If a tangent BC is drawn at a point R lying on the minor arc PQ to intersect AP at B and AQ at C, find the perimeter of the ∆ABC.
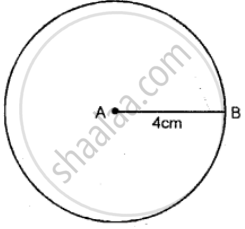
Mark two points A and B ,4cm a part, Draw a circle passing through B and with A as a center
Draw circle with the radii given below.
2 cm
If a chord AB subtends an angle of 60° at the centre of a circle, then angle between the tangents at A and B is also 60°.
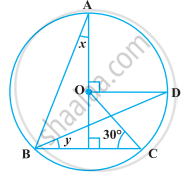
In the following figure, O is the centre of the circle, ∠BCO = 30°. Find x and y.
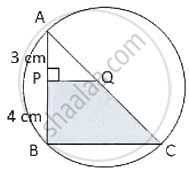
In the adjoining figure, AC is a diameter of the circle. AP = 3 cm and PB = 4 cm and QP ⊥ AB. If the area of ΔAPQ is 18 cm2, then the area of shaded portion QPBC is ______.