Advertisements
Advertisements
प्रश्न
A chord is at a distance of 15 cm from the centre of the circle of radius 25 cm. The length of the chord is
पर्याय
25 cm
20 cm
40 cm
18 cm
उत्तर
40 cm
Explanation;
Hint: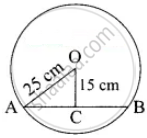
In the right triangle OAC,
AC2 = OA2 – OC2
= 252 – 152
= (25 + 15)(25 – 15)
= 40 × 10
AC2 = 400
AC = `sqrt(400)`
= 20
Length of the chord AB = 20 + 20 = 40 cm.
APPEARS IN
संबंधित प्रश्न
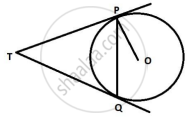
Two tangents TP and TQ are drawn to a circle with centre O from an external point T. Prove that ∠PTQ = 2∠OPQ.
If ΔABC is isosceles with AB = AC and C (0, 2) is the in circle of the ΔABC touching BC at L, prove that L, bisects BC.
Draw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points?
In the below fig. O is the centre of the circle. If ∠APB = 50°, find ∠AOB and ∠OAB.

In Fig. 4, an isosceles triangle ABC, with AB = AC, circumscribes a circle. Prove that the point of contact P bisects the base BC.
Find the diameter of the circle if the length of a chord is 3.2 cm and itd distance from the centre is 1.2 cm.
Use the figure given below to fill in the blank:
Diameter of a circle is ______.

In the figure, a circle with center P touches the semicircle at points Q and C having center O. If diameter AB = 10, AC = 6, then find the radius x of the smaller circle.
If a hexagon ABCDEF circumscribe a circle, prove that AB + CD + EF = BC + DE + FA.
If A, B, C, D are four points such that ∠BAC = 30° and ∠BDC = 60°, then D is the centre of the circle through A, B and C.
