Advertisements
Advertisements
Question
Tangents PA and PB are drawn from an external point P to two concentric circles with centre O and radii 8 cm and 5 cm respectively, as shown in Fig. 3. If AP = 15 cm, then find the length of BP.
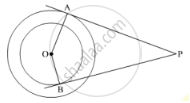
Solution
To find: BP
Construction: Join OP.
`Now ,OA _|_AP`and `OB_|_BP` `[therefore\text{Tangent to a circle is prependicular to the radius through the point of contact}]`
⇒ ∠OAP = ∠OBP = 90°
On applying Pythagoras theorem in ΔOAP, we obtain:
(OP)2 = (OA)2 + (AP)2
⇒ (OP)2 = (8)2 + (15)2
⇒ (OP)2 = 64 + 225
⇒ (OP)2 = 289
`rArr OP=sqrt289`
⇒ OP = 17
Thus, the length of OP is 17 cm.
On applying Pythagoras theorem in ΔOBP, we obtain:
(OP)2= (OB)2 + (BP)2
⇒ (17)2 = (5)2 + (BP)2
⇒ 289 = 25 + (BP)2
⇒ (BP)2 = 289 − 25
⇒ (BP)2 = 264
⇒ BP = 16.25 cm (approx.)
Hence, the length of BP is 16.25 cm.
RELATED QUESTIONS
In Fig., if AB = AC, prove that BE = EC
In two concentric circles, prove that all chords of the outer circle which touch the inner circle are of equal length.
If AB, AC, PQ are tangents in Fig. and AB = 5cm find the perimeter of ΔAPQ.
true or false
Sector is the region between the chord and its corresponding arc.
In the given figure, if ABC is an equilateral triangle. Find ∠BDC and ∠BEC.
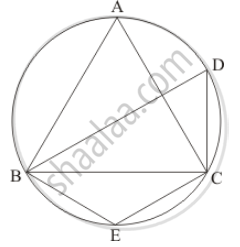
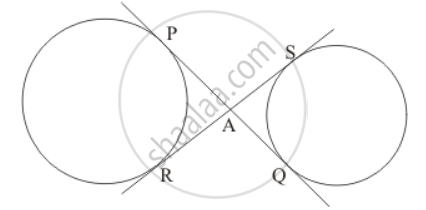
In the given figure, common tangents PQ and RS to two circles intersect at A. Prove that PQ = RS.
In the given figure, chord EF || chord GH. Prove that, chord EG ≅ chord FH. Fill in the blanks and write the proof.

If O is the center of the circle in the figure alongside, then complete the table from the given information.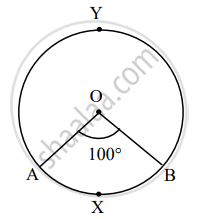
The type of arc
| Type of circular arc | Name of circular arc | Measure of circular arc |
| Minor arc | ||
| Major arc |
If an isosceles triangle ABC, in which AB = AC = 6 cm, is inscribed in a circle of radius 9 cm, find the area of the triangle.
In the following figure, BC is a diameter of the circle and ∠BAO = 60º. Then ∠ADC is equal to ______.