Advertisements
Advertisements
Question
Given: A circle inscribed in a right angled ΔABC. If ∠ACB = 90° and the radius of the circle is r.
To prove: 2r = a + b – c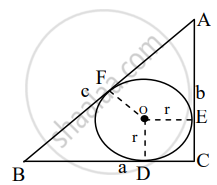
Solution
Proof: In given figure,
`{:("AF" = "AE"),("FB" = "BD"),("EC" = "DC"):}}` .....(i) [Tangent Segment theorem]
In ▢ODCE,
∠ECD = 90° ......[∠ACB = 90°, A–E–C, B-D–C]
`{:(∠"ODC" = 90^circ),(∠"OEC" = 90^circ):}}` ......[Tangent theorem]
∴ ∠EOD = 90° …[Ramining angle of ▢ODCE]
∴ ▢ODCE is a rectangle.
. Also, OE = OD = r ......[Radii of the same circle]
∴ ▢ODCE is a square ......`[("A Rectangle is square if it's"),("adjcent sides are congruent")]`
∴ OE = OD = CD = CE = r ......(ii) [sides of the square]
Consider R.H.S. = a + b – c
= BC + AC – AB
= (BD + DC) + (AE + EC) – (AF + FB) ......[B–D–C, A–E–C, A–F–B]
= (FB + r) + (AF + r) – (AF + FB) ......[From (i) and (ii)]
= FB + r + AF + r – AF - FB
= 2r
= L.H.S
∴ 2r = a + b – c
RELATED QUESTIONS
In the given figure, PQ is a chord of length 8cm of a circle of radius 5cm. The tangents at P and Q intersect at a point T. Find the length TP

From an external point P, tangents PA and PB are drawn to the circle with centre O. If CD is the tangent to the circle at point E and PA = 14 cm. Find the perimeter of ABCD.
In fig. a circle touches all the four sides of quadrilateral ABCD with AB = 6cm, BC = 7cm, CD = 4cm. Find AD.
In the fig two tangents AB and AC are drawn to a circle O such that ∠BAC = 120°. Prove that OA = 2AB.
In the given figure, if arc AB = arc CD, then prove that the quadrilateral ABCD is an isosceles– trapezium (O is the centre of the circle).
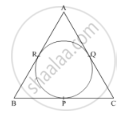
In Fig. 4, an isosceles triangle ABC, with AB = AC, circumscribes a circle. Prove that the point of contact P bisects the base BC.
In figure 1, O is the centre of a circle, PQ is a chord and PT is the tangent at P.
If ∠POQ = 70°, then ∠TPQ is equal to

In the given figure, ABC is a right triangle right-angled at B such that BC = 6 cm and AB = 8 cm. Find the radius of its incircle.

In the given figure, PO \[\perp\] QO. The tangents to the circle at P and Q intersect at a point T. Prove that PQ and OTare right bisector of each other.

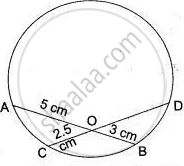
In Fig., chords AB and CD of the circle intersect at O. AO = 5 cm, BO = 3 cm and CO = 2.5 cm. Determine the length of DO.
All the radii of a circle are _______________
A, B, C are any points on the circle with centre O. If m(arc BC) = 110° and m(arc AB) = 125°, find measure arc AC.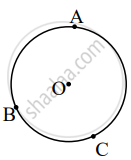
In the figure, a circle touches all the sides of quadrilateral ABCD from the inside. The center of the circle is O. If AD⊥ DC and BC = 38, QB = 27, DC = 25, then find the radius of the circle.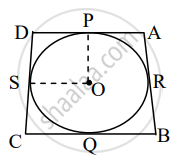
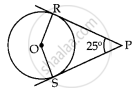
In the given figure, if ZRPS = 25°, the value of ZROS is ______
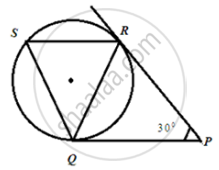
In the following figure, tangents PQ and PR are drawn to a circle such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ, then ∠RQS.
The tangent to the circumcircle of an isosceles triangle ABC at A, in which AB = AC, is parallel to BC.
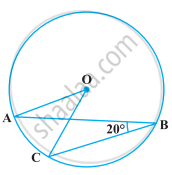
In the following figure, if ∠ABC = 20º, then ∠AOC is equal to ______.
In the following figure, ∠OAB = 30º and ∠OCB = 57º. Find ∠BOC and ∠AOC.

Is every diameter of a circle also a chord?
