Advertisements
Advertisements
प्रश्न
The incircle of an isosceles triangle ABC, in which AB = AC, touches the sides BC, CA and AB at D, E and F respectively. Prove that BD = DC.
उत्तर
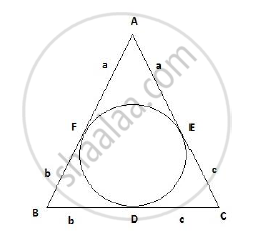
Given: ABC is an isosceles triangle in which AB = AC; with a circle inscribed
in the triangle.
To prove: BD = DC
Proof:
AF and AE are tangents drawn to the circle from point A.
Since two tangents drawn to a circle from the same exterior point are equal,
AF = AE = a
Similarly BF = BD = b and CD = CE = c
We also know that Δ ABC is an isosceles triangle in which AB = AC.
a+b = a+c
Thus b = c
Therefore, BD = DC
Hence proved.
APPEARS IN
संबंधित प्रश्न
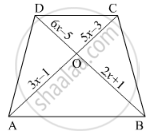
In the below figure, If AB || CD, find the value of x.
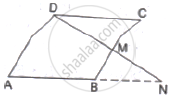
M is a point on the side BC of a parallelogram ABCD. DM when produced meets AB produced at N. Prove that
(1)` (DM)/(MN)=(DC)/(BN)`
(2)` (DN)/(DM)=(AN)/(DC)`
In the given figure, given that ∆ABC ∼ ∆PQR and quad ABCD ∼ quad PQRS. Determine the value of x, y, z in each case.

In the given figure,

AB || DC prove that
(i) ∆DMU ∼ ∆BMV
Corresponding sides of two similar triangles are in the ratio 1 : 3. If the area of the smaller triangle in 40 cm2, find the area of the larger triangle.
If the altitude of two similar triangles are in the ratio 2 : 3, what is the ratio of their areas?
State Pythagoras theorem and its converse.
In a ∆ABC, AD is the bisector of ∠BAC. If AB = 6 cm, AC = 5 cm and BD = 3 cm, then DC =
In an isosceles triangle ABC if AC = BC and AB2 = 2AC2, then ∠C =
D and E are respectively the points on the sides AB and AC of a triangle ABC such that AD = 2 cm, BD = 3 cm, BC = 7.5 cm and DE || BC. Then, length of DE (in cm) is ______.
