Advertisements
Advertisements
प्रश्न
In the given figure,

AB || DC prove that
(i) ∆DMU ∼ ∆BMV
उत्तर
(i) Given `AB||DC`
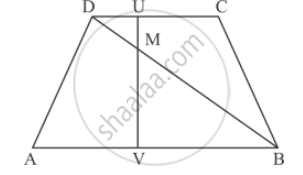
In triangle DMU and BMV, we have
`∠ MUD =∠ MVB`
Each angle is equal to 90°
`∠ UMD =∠ VMB`
Each are vertically opposite angles.
Therefore, by AA-criterion of similarity
` ∆DMU ∼ ∆BMV`
APPEARS IN
संबंधित प्रश्न
A girl of height 90 cm is walking away from the base of a lamp-post at a speed of 1.2m/sec. If the lamp is 3.6 m above the ground, find the length of her shadow after 4 seconds.
In a ΔABC, AD is the bisector of ∠A.
If AB = 5.6cm, BD = 3.2cm and BC = 6cm, find AC.
A 13m long ladder reaches a window of a building 12m above the ground. Determine the distance of the foot of the ladder from the building.
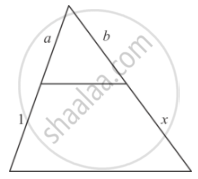
In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :
In ∆ABC, D and E are points on sides AB and AC respectively such that AD ✕ EC = AE ✕ DB. Prove that DE || BC.
State SSS similarity criterion.
State Pythagoras theorem and its converse.
If ∆ABC and ∆DEF are similar such that 2AB = DE and BC = 8 cm, then EF =
In ∆ABC, D and E are points on side AB and AC respectively such that DE || BC and AD : DB = 3 : 1. If EA = 3.3 cm, then AC =
A vertical stick 20 m long casts a shadow 10 m long on the ground. At the same time, a tower casts a shadow 50 m long on the ground. The height of the tower is
