Advertisements
Advertisements
प्रश्न
In the given figure,

AB || DC prove that
DM × BV = BM ✕ DU
उत्तर
Since ` ∆DMU ∼ ∆BMV`
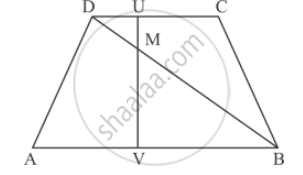
`(DM)/(BM)=(MU)/(MV)=(DU)/(BV)`
`(DM)/(BM)=(DU)/(BV)`
By cross multiplication, we get `DMxxBVxxDUxxBM`
Hence proved that `DMxxBVxxDUxxBM`
APPEARS IN
संबंधित प्रश्न
ABCD is a quadrilateral in which AD = BC. If P, Q, R, S be the mid-points of AB, AC, CD and BD respectively, show that PQRS is a rhombus.
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC
If AD = 3.6cm, AB = 10cm and AE = 4.5cm, find EC and AC.

In the given figure, given that ∆ABC ∼ ∆PQR and quad ABCD ∼ quad PQRS. Determine the value of x, y, z in each case.

In ∆ABC, ∠A = 60°. Prove that BC2 = AB2 + AC2 − AB . AC.
In ∆ABC, ∠C is an obtuse angle. AD ⊥ BC and AB2 = AC2 + 3 BC2. Prove that BC = CD.
In a quadrilateral ABCD, ∠B = 90°. If AD2 = AB2 + BC2 + CD2 then prove that ∠ACD = 90°.
The lengths of the diagonals of a rhombus are 30 cm and 40 cm. Find the side of the rhombus.
In the given figure, ∆AHK is similar to ∆ABC. If AK = 10 cm, BC = 3.5 cm and HK = 7 cm, find AC.

In a right triangle ABC right-angled at B, if P and Q are points on the sides AB and AC respectively, then
In an isosceles triangle ABC if AC = BC and AB2 = 2AC2, then ∠C =
