Advertisements
Advertisements
प्रश्न
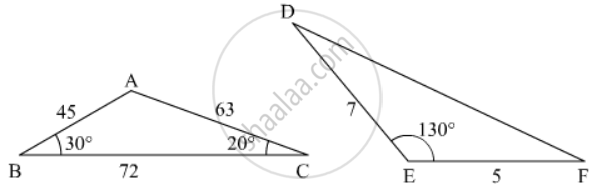
In a right triangle ABC right-angled at B, if P and Q are points on the sides AB and AC respectively, then
पर्याय
AQ2 + CP2 = 2(AC2 + PQ2)
2(AQ2 + CP2) = AC2 + PQ2
AQ2 + CP2 = AC2 + PQ2
\[AQ + CP = \frac{1}{2}\left( AC + PQ \right)\]
उत्तर
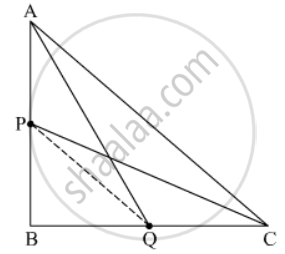
Applying Pythagoras theorem,
In ΔAQB,
In ΔPBC
`CP^2=PB^2+BC^2`..............(2)
Adding (1) and (2), we get
\[{AQ}^2 + {CP}^2 = {AB}^2 + {BQ}^2 + {PB}^2 + {BC}^2 \]....(3)
In ΔABC,
`AC^2=AB^2+BC^2`....(4)
In ΔPBQ,
From (3), (4) and (5), we get
We got the result as `c`
Notes
Disclaimer: There is mistake in the problem. The question should be "In a right triangle ABC right-angled at B, if P and Q are points on the sides AB and BC respectively, then"
Given: In the right ΔABC, right angled at B. P and Q are points on the sides AB and BC respectively.
APPEARS IN
संबंधित प्रश्न
the below given figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm, such that the segments BD and DC are respectively of lengths 6 cm and 9 cm. If the area of ΔABC is 54 cm2, then find the lengths of sides AB and AC.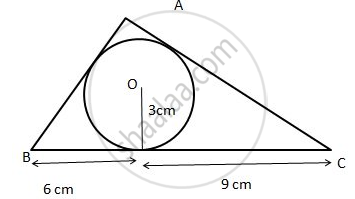
What values of x will make DE || AB in the given figure?

In ∆ABC, P and Q are points on sides AB and AC respectively such that PQ || BC. If AP = 4 cm, PB = 6 cm and PQ = 3 cm, determine BC.
In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.

ABCD is a trapezium in which AB || DC. P and Q are points on sides AD and BC such that PQ || AB. If PD = 18, BQ = 35 and QC = 15, find AD.
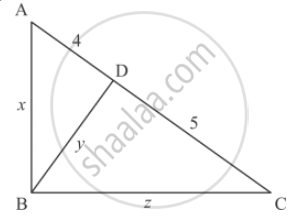
In each of the figures given below, an altitude is drawn to the hypotenuse by a right-angled triangle. The length of different line-segment are marked in each figure. Determine x, y, z in each case.
If ∆ABC and ∆DEF are two triangles such that\[\frac{AB}{DE} = \frac{BC}{EF} = \frac{CA}{FD} = \frac{3}{4}\], then write Area (∆ABC) : Area (∆DEF)
If in ∆ABC and ∆DEF, \[\frac{AB}{DE} = \frac{BC}{FD}\], then ∆ABC ∼ ∆DEF when
In an equilateral triangle ABC if AD ⊥ BC, then
In the given figure the measure of ∠D and ∠F are respectively