Advertisements
Advertisements
प्रश्न
If E is a point on side CA of an equilateral triangle ABC such that BE ⊥ CA, then AB2 + BC2 + CA2 =
पर्याय
2 BE2
3 BE2
4 BE2
6 BE2
उत्तर
In triangle ABC, E is a point on AC such that `BE ⊥ AC`.
We need to find `AB^2+BC^2+AC^2`.

Since `BE ⊥ AC`, CE = AE =
In triangle ABE, we have
`AB^2 = BE^2+AE^2`
Since AB = BC = AC
Therefore, `AB^2=BC^2=AC^2=BE^2+AE^2`
Since in triangle BE is an altitude, so `BE = (sqrt3)/2 AB`
`BE = (sqrt3)/2 AB`
`(sqrt3)/2 xxAC`
`(sqrt3)/2 xx 2AE= sqrt3AE`
`⇒ AB^2 + BC^2+AC^2= 3BE^2+3((BE)/sqrt3)^2`
`= 3BE^2+BE^2=4BE^2`
Hence option (c) is correct.
APPEARS IN
संबंधित प्रश्न
the below given figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm, such that the segments BD and DC are respectively of lengths 6 cm and 9 cm. If the area of ΔABC is 54 cm2, then find the lengths of sides AB and AC.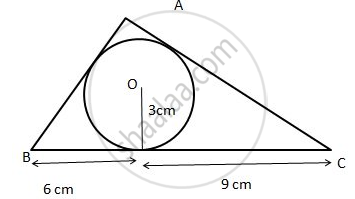
D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AD = 5.7cm, DB = 9.5cm, AE = 4.8cm and EC = 8cm.

In a ΔABC, AD is the bisector of ∠A.
If AB = 6.4cm, AC = 8cm and BD = 5.6cm, find DC.
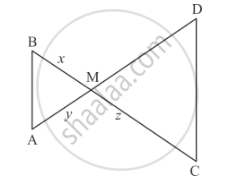
In the given figure, ∆AMB ∼ ∆CMD; determine MD in terms of x, y and z.
ABCD is a trapezium having AB || DC. Prove that O, the point of intersection of diagonals, divides the two diagonals in the same ratio. Also prove that
The area of two similar triangles are 36 cm2 and 100 cm2. If the length of a side of the smaller triangle in 3 cm, find the length of the corresponding side of the larger triangle.
State AAA similarity criterion.
The areas of two similar triangles are 169 cm2 and 121 cm2 respectively. If the longest side of the larger triangle is 26 cm, what is the length of the longest side of the smaller triangle?
∆ABC and ∆BDE are two equilateral triangles such that D is the mid-point of BC. The ratio of the areas of triangle ABC and BDE is
In a right triangle ABC right-angled at B, if P and Q are points on the sides AB and AC respectively, then
