Advertisements
Advertisements
प्रश्न
The area of two similar triangles are 36 cm2 and 100 cm2. If the length of a side of the smaller triangle in 3 cm, find the length of the corresponding side of the larger triangle.
उत्तर
Since the ratio of areas of two similar triangles is equal to the ratio of the squares of any two corresponding sides.
`\text{(Area of triangle)}/\text{(Area of larger triangle)}=\text{(Corresponding side of smaller triangle)}^2/\text{(Corresponding side of larger triangle)}^2`
`36/100=3^2/\text{(Corresponding side of larger triangle)}^2`
`\text{(Corresponding side of larger triangle)}^2= (9xx100)/(36)`
`\text{(Corresponding side of larger triangle)}^2 100/4`
`\text{(Corresponding side of larger triangle)}^2=25`
`\text{(Corresponding side of larger triangle)}^2= 5`
Hence, the length of the corresponding side of the larger triangle is `5 cm`
APPEARS IN
संबंधित प्रश्न
In the below figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm, such that the segments BD and DC are respectively of lengths 6 cm and 9 cm. If the area of Δ ABC is 54 cm2, then find the lengths of sides AB and AC.

In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :

In ∆ABC, points P and Q are on CA and CB, respectively such that CA = 16 cm, CP = 10 cm, CB = 30 cm and CQ = 25 cm. Is PQ || AB?
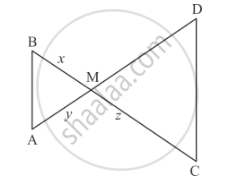
In the given figure, ∆AMB ∼ ∆CMD; determine MD in terms of x, y and z.
In ∆ABC, ∠C is an obtuse angle. AD ⊥ BC and AB2 = AC2 + 3 BC2. Prove that BC = CD.
If ∆ABC and ∆DEF are two triangles such tha\[\frac{AB}{DE} = \frac{BC}{EF} = \frac{CA}{FD} = \frac{2}{5}\] , then Area (∆ABC) : Area (∆DEF) =
If in two triangles ABC and DEF, \[\frac{AB}{DE} = \frac{BC}{FE} = \frac{CA}{FD}\], then
A chord of a circle of radius 10 cm subtends a right angle at the centre. The length of the chord (in cm) is
If ABC is an isosceles triangle and D is a point of BC such that AD ⊥ BC, then
∆ABC is such that AB = 3cm, BC = 2cm, CA = 2.5cm. If ∆ABC ~ ∆DEF and EF = 4cm, then perimeter of ∆DEF is ______.
