Advertisements
Advertisements
प्रश्न
In the below figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm, such that the segments BD and DC are respectively of lengths 6 cm and 9 cm. If the area of Δ ABC is 54 cm2, then find the lengths of sides AB and AC.

उत्तर


Let the given circle touch the sides AB and AC of the triangle at points F and E respectively and let the length of the line segment AF be x.
Now, it can be observed that:
BF = BD = 6 cm (tangents from point B)
CE = CD = 9 cm (tangents from point C)
AE = AF = x (tangents from point A)
AB = AF + FB = x + 6
BC = BD + DC = 6 + 9 = 15
CA = CE + EA = 9 + x
2s = AB + BC + CA = x + 6 + 15 + 9 + x = 30 + 2x
s = 15 + x
s – a = 15 + x – 15 = x
s – b = 15 + x – (x + 9) = 6
s – c = 15 + x – (6 + x) = 9
`"Area of " triangleABC =sqrt(s(s-a)(s-b)(s-c))`
`54=sqrt((15+x)(x)(6)(9))`
`54=3sqrt(6(15x+x^2))`
`18=sqrt(6(15x+x^2))`
`324=6(15x+x^2)`
`54=15x+x^2`
`x^2+15x-54=0`
`x^2+18x-3x-54=0`
x(x+18)-3(x+18)=0
(x+18)(x-3)=0
x = -18 and x = 3
As distance cannot be negative, x = 3
AC = 3 + 9 = 12
AB = AF + FB = 6 + x = 6 + 3 = 9
APPEARS IN
संबंधित प्रश्न
In below Figure, ΔABC is right angled at C and DE ⊥ AB. Prove that ΔABC ~ ΔADE and Hence find the lengths of AE and DE.

A ladder is placed in such a way that its foot is at a distance of 15m from a wall and its top reaches a window 20m above the ground. Find the length of the ladder.
In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.

In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.
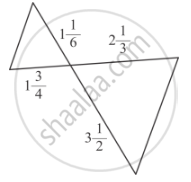
In ∆ABC, ray AD bisects ∠A and intersects BC in D. If BC = a, AC = b and AC = c, prove that \[DC = \frac{ab}{b + c}\]
If ∆ABC and ∆DEF are two triangles such that\[\frac{AB}{DE} = \frac{BC}{EF} = \frac{CA}{FD} = \frac{3}{4}\], then write Area (∆ABC) : Area (∆DEF)
State Pythagoras theorem and its converse.
The areas of two similar triangles ∆ABC and ∆DEF are 144 cm2 and 81 cm2 respectively. If the longest side of larger ∆ABC be 36 cm, then the longest side of the smaller triangle ∆DEF is
If ∆ABC and ∆DEF are two triangles such tha\[\frac{AB}{DE} = \frac{BC}{EF} = \frac{CA}{FD} = \frac{2}{5}\] , then Area (∆ABC) : Area (∆DEF) =
In a ∆ABC, ∠A = 90°, AB = 5 cm and AC = 12 cm. If AD ⊥ BC, then AD =
