Advertisements
Advertisements
प्रश्न
In below Figure, ΔABC is right angled at C and DE ⊥ AB. Prove that ΔABC ~ ΔADE and Hence find the lengths of AE and DE.

उत्तर
In ΔACB, by Pythagoras theorem
AB2 = AC2 + BC2
⇒ AB2 = (5)2 + (12)2
⇒ AB2 = 25 + 144 = 169
⇒ AB = `sqrt169` = 13 cm
In ΔAED and ΔACB
∠A = ∠A [Common]
∠AED = ∠ACB [Each 90°]
Then, ΔAED ~ ΔACB [By AA similarity]
`therefore"AE"/"AC"="DE"/"CB"="AD"/"AB"` [Corresponding parts of similar Δ are proportional]
`rArr"AE"/5="DE"/12=3/13`
`rArr"AE"/5=3/13` and `"DE"/12=3/13`
`"AE"=15/13` cm and `"DE"=36/13` cm
APPEARS IN
संबंधित प्रश्न
D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AD = 5.7cm, DB = 9.5cm, AE = 4.8cm and EC = 8cm.

In ∆ABC, D and E are points on sides AB and AC respectively such that AD ✕ EC = AE ✕ DB. Prove that DE || BC.
There is a staircase as shown in the given figure, connecting points A and B. Measurements of steps are marked in the figure. Find the straight line distance between A and B.

In the adjoining figure, if AD is the bisector of ∠A, what is AC?
State AAA similarity criterion.
In the given figure, S and T are points on the sides PQ and PR respectively of ∆PQR such that PT = 2 cm, TR = 4 cm and ST is parallel to QR. Find the ratio of the areas of ∆PST and ∆PQR.

In a ∆ABC, AD is the bisector of ∠BAC. If AB = 6 cm, AC = 5 cm and BD = 3 cm, then DC =
∆ABC ∼ ∆DEF, ar(∆ABC) = 9 cm2, ar(∆DEF) = 16 cm2. If BC = 2.1 cm, then the measure of EF is
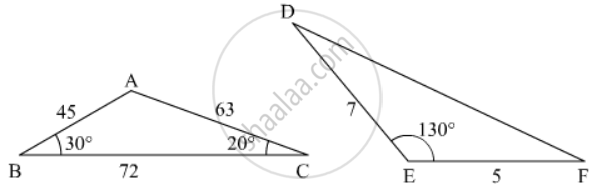
In the given figure the measure of ∠D and ∠F are respectively
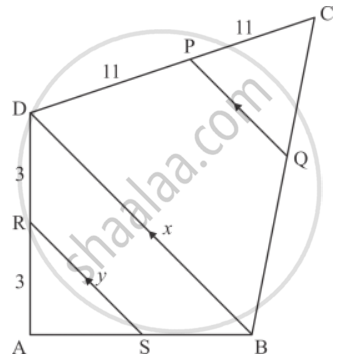
In the given figure, RS || DB || PQ. If CP = PD = 11 cm and DR = RA = 3 cm. Then the values of x and y are respectively.