Advertisements
Advertisements
प्रश्न
In the given figure, S and T are points on the sides PQ and PR respectively of ∆PQR such that PT = 2 cm, TR = 4 cm and ST is parallel to QR. Find the ratio of the areas of ∆PST and ∆PQR.

उत्तर
Given: In ΔPQR, S and T are the points on the sides PQ and PR respectively such that PT = 2cm, TR = 4cm and ST is parallel to QR.
To find: Ratio of areas of ΔPST and ΔPQR
\[In ∆ PST and ∆ PQR, \]
\[\angle PST = \angle Q \left( \text{Corresponding angles} \right)\]
\[\angle P = \angle P \left( \text{Common} \right)\]
\[ \therefore ∆ PST ~ ∆ PQR \left( AA \hspace{0.167em} \text{Similarity} \right)\]
Now, we know that the areas of two similar triangles are in the ratio of the squares of the corresponding sides. Therefore,
`(Area(Δ PST))/(Area(Δ PQR))= (PT^2)/(PR^2)`
`(Area(Δ PST))/(Area(Δ PQR))= (PT^2)/(PT+TR)^2`
`(Area(Δ PST))/(Area(Δ PQR))= (2^2)/(2+4)^2`
`(Area(Δ PST))/(Area(Δ PQR))= 4/36=1/9`
APPEARS IN
संबंधित प्रश्न
In below figure, If AB || CD, find the value of x.
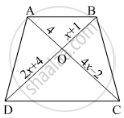
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC
If AD = 3.6cm, AB = 10cm and AE = 4.5cm, find EC and AC.

In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :

In ∆ABC, P and Q are points on sides AB and AC respectively such that PQ || BC. If AP = 4 cm, PB = 6 cm and PQ = 3 cm, determine BC.
The area of two similar triangles are 36 cm2 and 100 cm2. If the length of a side of the smaller triangle in 3 cm, find the length of the corresponding side of the larger triangle.
State basic proportionality theorem and its converse.
The areas of two similar triangles ∆ABC and ∆DEF are 144 cm2 and 81 cm2 respectively. If the longest side of larger ∆ABC be 36 cm, then the longest side of the smaller triangle ∆DEF is
If D, E, F are the mid-points of sides BC, CA and AB respectively of ∆ABC, then the ratio of the areas of triangles DEF and ABC is
A man goes 24 m due west and then 7 m due north. How far is he from the starting point?
If ∆ABC ∼ ∆DEF such that DE = 3 cm, EF = 2 cm, DF = 2.5 cm, BC = 4 cm, then perimeter of ∆ABC is
