Advertisements
Advertisements
प्रश्न
The areas of two similar triangles ∆ABC and ∆DEF are 144 cm2 and 81 cm2 respectively. If the longest side of larger ∆ABC be 36 cm, then the longest side of the smaller triangle ∆DEF is
पर्याय
20 cm
26 cm
27 cm
30 cm
उत्तर
Given: Areas of two similar triangles ΔABC and ΔDEF are 144cm2 and 81cm2.
If the longest side of larger ΔABC is 36cm
To find: the longest side of the smaller triangle ΔDEF
We know that the ratio of areas of two similar triangles is equal to the ratio of squares of their corresponding sides.
`\text{ar(Δ ABC)}/\text{ar(Δ DEF)}=(\text{longest side of larger Δ ABC}/\text{longest side of smaller Δ DEF})^2`
`114/81=(36/\text{longest side of smaller Δ DEF})^2`
Taking square root on both sides, we get
`\text{longest side of smaller Δ DEF}=(36xx9)/12=27cm`
Hence the correct answer is `C`
APPEARS IN
संबंधित प्रश्न
D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AD = 5.7cm, DB = 9.5cm, AE = 4.8cm and EC = 8cm.

D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AD = 7.2cm, AE = 6.4cm, AB = 12cm and AC = 10cm.
In a ΔABC, AD is the bisector of ∠A.
If AB = 5.6cm, AC = 4cm and DC = 3cm, find BC.

In ∆PQR, M and N are points on sides PQ and PR respectively such that PM = 15 cm and NR = 8 cm. If PQ = 25 cm and PR = 20 cm state whether MN || QR.
In ∆ABC, AD and BE are altitude. Prove that\[\frac{ar\left( ∆ DEC \right)}{ar\left( ∆ ABC \right)} = \frac{{DC}^2}{{AC}^2}\]
In ∆ABC, if BD ⊥ AC and BC2 = 2 AC . CD, then prove that AB = AC.
In ∆ABC, AD is a median. Prove that AB2 + AC2 = 2AD2 + 2DC2.
State AAA similarity criterion.
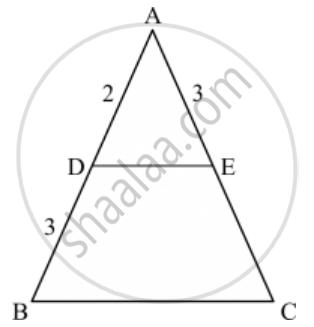
In the given figure, if ∠ADE = ∠ABC, then CE =
If ABC is an isosceles triangle and D is a point of BC such that AD ⊥ BC, then
