Advertisements
Advertisements
Question
The areas of two similar triangles ∆ABC and ∆DEF are 144 cm2 and 81 cm2 respectively. If the longest side of larger ∆ABC be 36 cm, then the longest side of the smaller triangle ∆DEF is
Options
20 cm
26 cm
27 cm
30 cm
Solution
Given: Areas of two similar triangles ΔABC and ΔDEF are 144cm2 and 81cm2.
If the longest side of larger ΔABC is 36cm
To find: the longest side of the smaller triangle ΔDEF
We know that the ratio of areas of two similar triangles is equal to the ratio of squares of their corresponding sides.
`\text{ar(Δ ABC)}/\text{ar(Δ DEF)}=(\text{longest side of larger Δ ABC}/\text{longest side of smaller Δ DEF})^2`
`114/81=(36/\text{longest side of smaller Δ DEF})^2`
Taking square root on both sides, we get
`\text{longest side of smaller Δ DEF}=(36xx9)/12=27cm`
Hence the correct answer is `C`
APPEARS IN
RELATED QUESTIONS
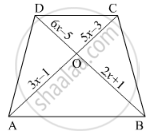
In the below figure, If AB || CD, find the value of x.
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC
If AD = 3.6cm, AB = 10cm and AE = 4.5cm, find EC and AC.

A ladder is placed in such a way that its foot is at a distance of 15m from a wall and its top reaches a window 20m above the ground. Find the length of the ladder.
In ∆ABC, P and Q are points on sides AB and AC respectively such that PQ || BC. If AP = 4 cm, PB = 6 cm and PQ = 3 cm, determine BC.
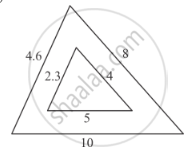
In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.
In the given figure, l || m
(i) Name three pairs of similar triangles with proper correspondence; write similarities.
(ii) Prove that

In ∆ABC, ∠A = 60°. Prove that BC2 = AB2 + AC2 − AB . AC.
In a quadrilateral ABCD, ∠B = 90°. If AD2 = AB2 + BC2 + CD2 then prove that ∠ACD = 90°.
In triangles ABC and DEF, ∠A = ∠E = 40°, AB : ED = AC : EF and ∠F = 65°, then ∠B =
In an isosceles triangle ABC if AC = BC and AB2 = 2AC2, then ∠C =
