Advertisements
Advertisements
Question
In ∆ABC, P and Q are points on sides AB and AC respectively such that PQ || BC. If AP = 4 cm, PB = 6 cm and PQ = 3 cm, determine BC.
Solution
In triangle ABC, P and Q are points on sides AB and AC respectively such that `PQ|| BC`.
In ΔAPQ and ΔABC,
Substituting value AP = 3cm,AB=10cm and PQ = 3cm, we get
`(AP)/(AB)=(3)/(BC)`
By cross multiplication we get
`4 xx BC = 3xx10`
`BC = (3xx10)/4`
`BC = 30/4`
`BC = 7.5 cm`
Hence, the value of BC is 7.5 cm.
APPEARS IN
RELATED QUESTIONS
In below Figure, ΔABC is right angled at C and DE ⊥ AB. Prove that ΔABC ~ ΔADE and Hence find the lengths of AE and DE.

In a ΔABC, AD is the bisector of ∠A.
If AB = 10cm, AC = 14cm and BC = 6cm, find BD and DC.
If ∆ABC and ∆DEF are two triangles such that\[\frac{AB}{DE} = \frac{BC}{EF} = \frac{CA}{FD} = \frac{3}{4}\], then write Area (∆ABC) : Area (∆DEF)
In the given figure, PQ || BC and AP : PB = 1 : 2. Find\[\frac{area \left( ∆ APQ \right)}{area \left( ∆ ABC \right)}\]

Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio.
The areas of two similar triangles are in respectively 9 cm2 and 16 cm2. The ratio of their corresponding sides is ______.
In a ∆ABC, AD is the bisector of ∠BAC. If AB = 6 cm, AC = 5 cm and BD = 3 cm, then DC =
If in ∆ABC and ∆DEF, \[\frac{AB}{DE} = \frac{BC}{FD}\], then ∆ABC ∼ ∆DEF when
In the given figure, the value of x for which DE || AB is
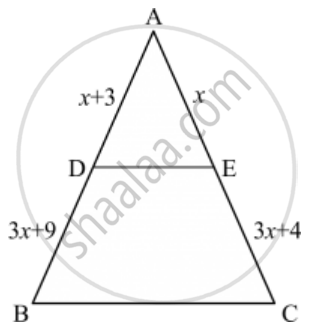
In the given figure, RS || DB || PQ. If CP = PD = 11 cm and DR = RA = 3 cm. Then the values of x and y are respectively.