Advertisements
Advertisements
Question
In the given figure, the value of x for which DE || AB is
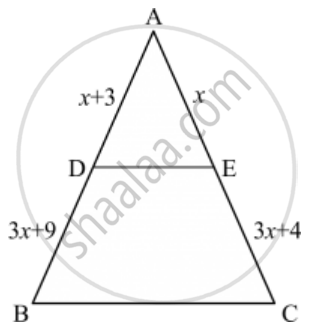
Options
4
1
3
2
Solution
Given: In ∆ABC, DE || AB.
To find: the value of x
According to basic proportionality theorem if a line is drawn parallel to one side of a triangle intersecting the other two sides, then it divides the two sides in the same ratio.
In ∆ABC, DE || AB
`(AD)/(DB)=(AE)/(EC)`
`(x+3)/(3x+19)=(x)/(3x+4)`
`(x+3)(3x+4)=(x)=(3x+19)`
`3x^2+4x+9x+12=3x^2+19x`
`19x-13x=12`
`6x=12`
`x=2`
Hence we got the result `d`.
APPEARS IN
RELATED QUESTIONS
A girl of height 90 cm is walking away from the base of a lamp-post at a speed of 1.2m/sec. If the lamp is 3.6 m above the ground, find the length of her shadow after 4 seconds.
A vertical stick of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.

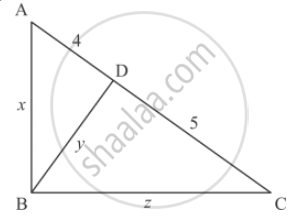
In each of the figures given below, an altitude is drawn to the hypotenuse by a right-angled triangle. The length of different line-segment are marked in each figure. Determine x, y, z in each case.
In ∆ABC, ∠C is an obtuse angle. AD ⊥ BC and AB2 = AC2 + 3 BC2. Prove that BC = CD.
If the areas of two similar triangles ABC and PQR are in the ratio 9 : 16 and BC = 4.5 cm, what is the length of QR?
In the given figure, DE || BC and \[AD = \frac{1}{2}BD\]. If BC = 4.5 cm, find DE.
If ABC and DEF are similar triangles such that ∠A = 47° and ∠E = 83°, then ∠C =
In a ∆ABC, ∠A = 90°, AB = 5 cm and AC = 12 cm. If AD ⊥ BC, then AD =
If E is a point on side CA of an equilateral triangle ABC such that BE ⊥ CA, then AB2 + BC2 + CA2 =
