Advertisements
Advertisements
Question
In the given figure, DE || BC and \[AD = \frac{1}{2}BD\]. If BC = 4.5 cm, find DE.
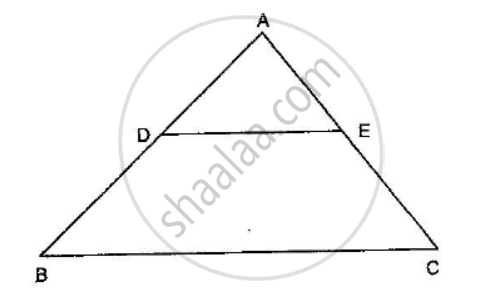
Solution
Given: In ∆ABC, DE || BC. `AD = 1/2BD` and BC = 4.5 cm.
To find: DE
In ∆ABC and ∆ADE
\[\angle B = \angle ADE \left( \text{Corresponding angles} \right)\]
\[\angle A = \angle A \left( \text{Common} \right)\]
\[ \therefore ∆ ABC~ ∆ ADE \left( \text{AA Similarity} \right)\]
`(AD)/(AB)=(DE)/(BC)`
`(AD)/(AD+BD)=(DE)/(BC)`
`(1/2BD)/(1/2+BD+BD)=(DE)/(BC)`
`1/3=(DE)/(BC)`
`1/3=(DE)/4.5`
`DE=1.5 cm`
APPEARS IN
RELATED QUESTIONS
In an isosceles ΔABC, the base AB is produced both the ways to P and Q such that AP × BQ = AC2. Prove that ΔAPC ~ ΔBCQ.
In a ΔABC, AD is the bisector of ∠A.
If AB = 5.6cm, BD = 3.2cm and BC = 6cm, find AC.
In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.
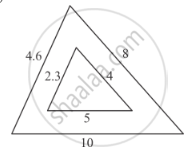
In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.

In the given figure,

AB || DC prove that
(i) ∆DMU ∼ ∆BMV
In a triangle ABC, N is a point on AC such that BN ⊥ AC. If BN2 = AN . NC, prove that ∠B = 90°.
∆ABC and ∆BDE are two equilateral triangles such that D is the mid-point of BC. The ratio of the areas of triangle ABC and BDE is
If ABC and DEF are similar triangles such that ∠A = 47° and ∠E = 83°, then ∠C =
The length of the hypotenuse of an isosceles right triangle whose one side is\[4\sqrt{2} cm\]
The areas of two similar triangles are 121 cm2 and 64 cm2 respectively. If the median of the first triangle is 12.1 cm, then the corresponding median of the other triangle is
