Advertisements
Advertisements
प्रश्न
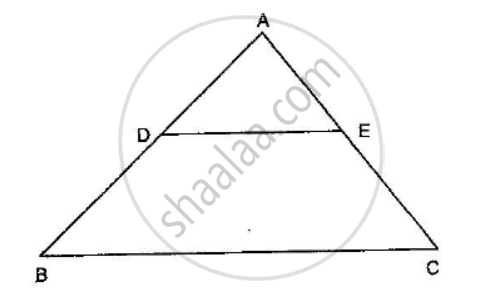
In the given figure, DE || BC and \[AD = \frac{1}{2}BD\]. If BC = 4.5 cm, find DE.
उत्तर
Given: In ∆ABC, DE || BC. `AD = 1/2BD` and BC = 4.5 cm.
To find: DE
In ∆ABC and ∆ADE
\[\angle B = \angle ADE \left( \text{Corresponding angles} \right)\]
\[\angle A = \angle A \left( \text{Common} \right)\]
\[ \therefore ∆ ABC~ ∆ ADE \left( \text{AA Similarity} \right)\]
`(AD)/(AB)=(DE)/(BC)`
`(AD)/(AD+BD)=(DE)/(BC)`
`(1/2BD)/(1/2+BD+BD)=(DE)/(BC)`
`1/3=(DE)/(BC)`
`1/3=(DE)/4.5`
`DE=1.5 cm`
APPEARS IN
संबंधित प्रश्न
A girl of height 90 cm is walking away from the base of a lamp-post at a speed of 1.2m/sec. If the lamp is 3.6 m above the ground, find the length of her shadow after 4 seconds.
D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AB = 10.8cm, AD = 6.3cm, AC = 9.6cm and EC = 4cm.
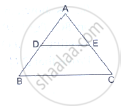
In ∆ABC, points P and Q are on CA and CB, respectively such that CA = 16 cm, CP = 10 cm, CB = 30 cm and CQ = 25 cm. Is PQ || AB?
In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.

The area of two similar triangles are 36 cm2 and 100 cm2. If the length of a side of the smaller triangle in 3 cm, find the length of the corresponding side of the larger triangle.
In ∆ABC, ray AD bisects ∠A and intersects BC in D. If BC = a, AC = b and AC = c, prove that \[BD = \frac{ac}{b + c}\]
In the adjoining figure, DE is parallel to BC and AD = 1 cm, BD = 2 cm. What is the ratio of the area of ∆ABC to the area of ∆ADE?
∆ABC is an isosceles triangle in which ∠C = 90. If AC = 6 cm, then AB =
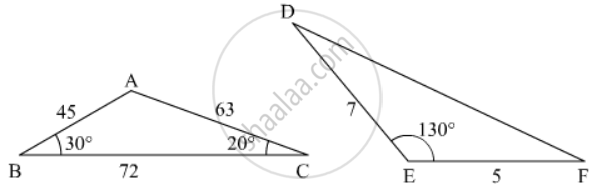
In the given figure the measure of ∠D and ∠F are respectively
∆ABC is a right triangle right-angled at A and AD ⊥ BC. Then, \[\frac{BD}{DC} =\]
