Question

∆ABC is a right triangle right-angled at A and  AD ⊥ BC. Then, \[\frac{BD}{DC} =\]

पर्याय

• \[\left( \frac{AB}{AC} \right)^2\]
• \[\frac{AB}{AC}\]
• \[\left( \frac{AB}{AD} \right)^2\]
• \[\frac{AB}{AD}\]

• Non of the above

Answer 1

Given: In ΔABC, `∠A = 90^o` and `AD ⊥ BC`.

To find: BD: DC

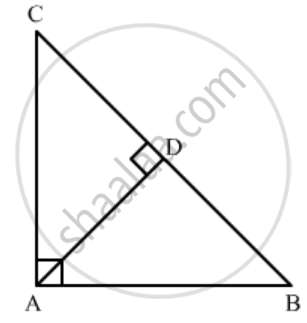
\[\angle CAD + \angle BAD = 90^o . . . . . \left( 1 \right)\]
\[\angle BAD + \angle ABD = 90^o. . . . . \left( 2 \right) \left( \angle ADB = 90^o \right)\]
\[\text{From (1) and (2)}, \]
\[\angle CAD = \angle ABD\]

In ΔADB and ΔADC,

\[\angle ADB = \angle ADC \left( 90^o \text{each} \right)\]
\[\angle ABD = \angle CAD \left( \text{Proved} \right)\]
\[ \therefore ∆ ADB~ ∆ ADC \left( \text{AA Similarity} \right)\]
\[ \Rightarrow \frac{CD}{AD} = \frac{AC}{AB} = \frac{AD}{BD} \left( \text{Corresponding sides are proportional} \right)\]

Disclaimer: The question is not correct. The given ratio cannot be evaluated using the given conditions in the question.