Advertisements
Advertisements
प्रश्न
∆ABC is a right triangle right-angled at A and AD ⊥ BC. Then, \[\frac{BD}{DC} =\]
विकल्प
- \[\left( \frac{AB}{AC} \right)^2\]
- \[\frac{AB}{AC}\]
- \[\left( \frac{AB}{AD} \right)^2\]
- \[\frac{AB}{AD}\]
Non of the above
उत्तर
Given: In ΔABC, `∠A = 90^o` and `AD ⊥ BC`.
To find: BD: DC
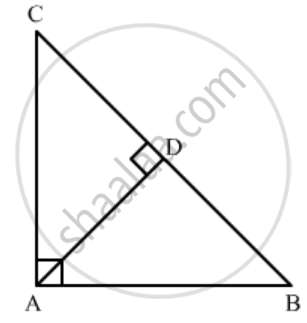
\[\angle CAD + \angle BAD = 90^o . . . . . \left( 1 \right)\]
\[\angle BAD + \angle ABD = 90^o. . . . . \left( 2 \right) \left( \angle ADB = 90^o \right)\]
\[\text{From (1) and (2)}, \]
\[\angle CAD = \angle ABD\]
In ΔADB and ΔADC,
\[\angle ABD = \angle CAD \left( \text{Proved} \right)\]
\[ \therefore ∆ ADB~ ∆ ADC \left( \text{AA Similarity} \right)\]
\[ \Rightarrow \frac{CD}{AD} = \frac{AC}{AB} = \frac{AD}{BD} \left( \text{Corresponding sides are proportional} \right)\]
APPEARS IN
संबंधित प्रश्न
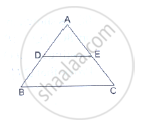
D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AD = 7.2cm, AE = 6.4cm, AB = 12cm and AC = 10cm.
In the given figure,

AB || DC prove that
DM × BV = BM ✕ DU
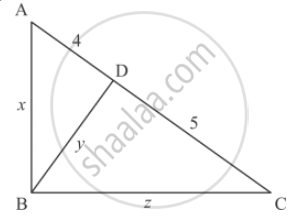
In each of the figures given below, an altitude is drawn to the hypotenuse by a right-angled triangle. The length of different line-segment are marked in each figure. Determine x, y, z in each case.
In ∆ABC, given that AB = AC and BD ⊥ AC. Prove that BC2 = 2 AC. CD
In ∆ABC, ∠ABC = 135°. Prove that AC2 = AB2 + BC2 + 4 ar (∆ABC)
State AAA similarity criterion.
A man goes 24 m due west and then 7 m due north. How far is he from the starting point?
∆ABC ∼ ∆PQR such that ar(∆ABC) = 4 ar(∆PQR). If BC = 12 cm, then QR =
∆ABC is an isosceles triangle in which ∠C = 90. If AC = 6 cm, then AB =
In an isosceles triangle ABC if AC = BC and AB2 = 2AC2, then ∠C =
