Advertisements
Advertisements
प्रश्न
State AAA similarity criterion.
उत्तर
AAA Similarity Criterion: If two triangles are equiangular, then they are similar.
In ΔABC and ΔDEF, if
`∠A=∠D`
`∠B=∠E`
`∠ C = ∠F`
Then, ΔABC ∼ Δ DEF
APPEARS IN
संबंधित प्रश्न
In the below figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm, such that the segments BD and DC are respectively of lengths 6 cm and 9 cm. If the area of Δ ABC is 54 cm2, then find the lengths of sides AB and AC.

In below Figure, ΔABC is right angled at C and DE ⊥ AB. Prove that ΔABC ~ ΔADE and Hence find the lengths of AE and DE.

In ∆PQR, M and N are points on sides PQ and PR respectively such that PM = 15 cm and NR = 8 cm. If PQ = 25 cm and PR = 20 cm state whether MN || QR.
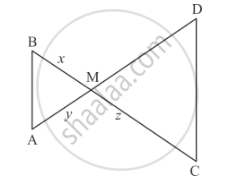
In the given figure, ∆AMB ∼ ∆CMD; determine MD in terms of x, y and z.
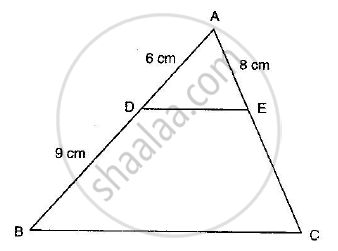
In the adjoining figure, find AC.
If ∆ABC and ∆DEF are two triangles such that\[\frac{AB}{DE} = \frac{BC}{EF} = \frac{CA}{FD} = \frac{3}{4}\], then write Area (∆ABC) : Area (∆DEF)
In the given figure, DE || BC and \[AD = \frac{1}{2}BD\]. If BC = 4.5 cm, find DE.
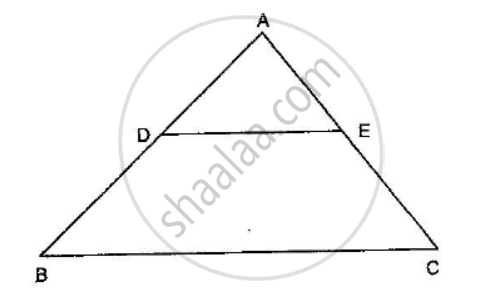
If D, E, F are the mid-points of sides BC, CA and AB respectively of ∆ABC, then the ratio of the areas of triangles DEF and ABC is
∆ABC ∼ ∆DEF. If BC = 3 cm, EF = 4 cm and ar(∆ABC) = 54 cm2, then ar(∆DEF) =
If ∆ABC ∼ ∆DEF such that DE = 3 cm, EF = 2 cm, DF = 2.5 cm, BC = 4 cm, then perimeter of ∆ABC is
