Advertisements
Advertisements
प्रश्न
If ∆ABC ∼ ∆DEF such that DE = 3 cm, EF = 2 cm, DF = 2.5 cm, BC = 4 cm, then perimeter of ∆ABC is
विकल्प
18 cm
20 cm
12 cm
15 cm
उत्तर
Given: ΔABC and ΔDEF are similar triangles such that DE = 3cm, EF = 2cm, DF = 2.5cm and BC = 4cm.
To find: Perimeter of ΔABC.
We know that if two triangles are similar then their corresponding sides are proportional.
Hence, `(AB)/(DE)=(BC)/(EF)=(CA)/(FD)`
Substituting the values we get
`(AB)/(BC)=(DE)/(EF)`
`(AB)/4=3/2`
`AB=6cm`..................(1)
Similarly,
`(CA)/(BE)=(DF)/(EF)`
`(CA)/4=2.5/2`
`CA=5cm`
Perimeter of Δ ABC = AB+BC+CA
= 6+4+5
= 15 cm
Hence the correct option is `d`
APPEARS IN
संबंधित प्रश्न
D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AD = 5.7cm, DB = 9.5cm, AE = 4.8cm and EC = 8cm.

In ∆PQR, M and N are points on sides PQ and PR respectively such that PM = 15 cm and NR = 8 cm. If PQ = 25 cm and PR = 20 cm state whether MN || QR.
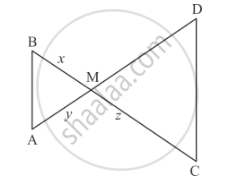
In the given figure, ∆AMB ∼ ∆CMD; determine MD in terms of x, y and z.
In the given figure,

AB || DC prove that
DM × BV = BM ✕ DU
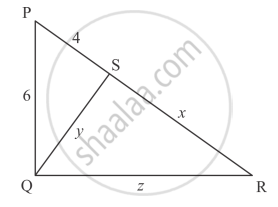
In each of the figures given below, an altitude is drawn to the hypotenuse by a right-angled triangle. The length of different line-segment are marked in each figure. Determine x, y, z in each case.
In ∆ABC, ∠C is an obtuse angle. AD ⊥ BC and AB2 = AC2 + 3 BC2. Prove that BC = CD.
The areas of two similar triangles are 169 cm2 and 121 cm2 respectively. If the longest side of the larger triangle is 26 cm, what is the length of the longest side of the smaller triangle?
In a ∆ABC, AD is the bisector of ∠BAC. If AB = 6 cm, AC = 5 cm and BD = 3 cm, then DC =
In an equilateral triangle ABC if AD ⊥ BC, then AD2 =
If ∆ABC ∼ ∆DEF such that AB = 9.1 cm and DE = 6.5 cm. If the perimeter of ∆DEF is 25 cm, then the perimeter of ∆ABC is
