Advertisements
Advertisements
प्रश्न
In an equilateral triangle ABC if AD ⊥ BC, then AD2 =
विकल्प
CD2
2CD2
3CD2
4CD2
उत्तर
In an equilateral ΔABC, `AD ⊥ BC`.
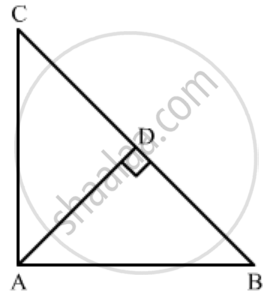
In ΔADC, applying Pythagoras theorem, we get
`AC^2=AD^2+DC^2`
`BC^2=AD^2+DC^2(∵ AC=BC)`
`(2DC)^2=AD^2+DC^2(∵ BC=2DC)`
`4DC^2=AD^2+DC^2`
`3DC^2=AD^2`
Hence, the correct option is (c).
APPEARS IN
संबंधित प्रश्न
Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using similarity criterion for two triangles, show that `"OA"/"OC"="OB"/"OD"`.
A vertical stick of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
A ladder is placed in such a way that its foot is at a distance of 15m from a wall and its top reaches a window 20m above the ground. Find the length of the ladder.
In ∆ABC, points P and Q are on CA and CB, respectively such that CA = 16 cm, CP = 10 cm, CB = 30 cm and CQ = 25 cm. Is PQ || AB?
In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.

In a quadrilateral ABCD, given that ∠A + ∠D = 90°. Prove that AC2 + BD2 = AD2 + BC2.
In ∆ABC, D and E are points on side AB and AC respectively such that DE || BC and AD : DB = 3 : 1. If EA = 3.3 cm, then AC =
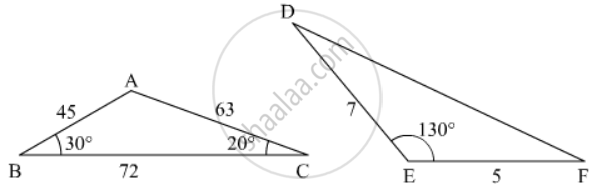
In the given figure the measure of ∠D and ∠F are respectively
In ∆ABC, a line XY parallel to BC cuts AB at X and AC at Y. If BY bisects ∠XYC, then
D and E are respectively the points on the sides AB and AC of a triangle ABC such that AD = 2 cm, BD = 3 cm, BC = 7.5 cm and DE || BC. Then, length of DE (in cm) is ______.
