Advertisements
Advertisements
Question
In an equilateral triangle ABC if AD ⊥ BC, then AD2 =
Options
CD2
2CD2
3CD2
4CD2
Solution
In an equilateral ΔABC, `AD ⊥ BC`.
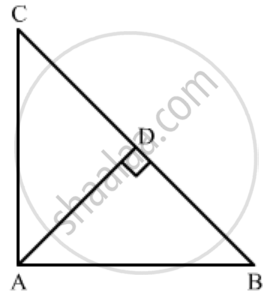
In ΔADC, applying Pythagoras theorem, we get
`AC^2=AD^2+DC^2`
`BC^2=AD^2+DC^2(∵ AC=BC)`
`(2DC)^2=AD^2+DC^2(∵ BC=2DC)`
`4DC^2=AD^2+DC^2`
`3DC^2=AD^2`
Hence, the correct option is (c).
APPEARS IN
RELATED QUESTIONS
In the below figure, If AB || CD, find the value of x.
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC
If AD = 3.6cm, AB = 10cm and AE = 4.5cm, find EC and AC.

In ∆ABC, points P and Q are on CA and CB, respectively such that CA = 16 cm, CP = 10 cm, CB = 30 cm and CQ = 25 cm. Is PQ || AB?
In the given figure, given that ∆ABC ∼ ∆PQR and quad ABCD ∼ quad PQRS. Determine the value of x, y, z in each case.

In the figure given below DE || BC. If AD = 2.4 cm, DB = 3.6 cm, AC = 5 cm. Find AE.
A man goes 24 m due west and then 7 m due north. How far is he from the starting point?
∆ABC is an isosceles triangle in which ∠C = 90. If AC = 6 cm, then AB =
If in two triangle ABC and DEF, ∠A = ∠E, ∠B = ∠F, then which of the following is not true?
(a)\[\frac{BC}{DF} = \frac{AC}{DE}\]
(b)\[\frac{AB}{DE} = \frac{BC}{DF}\]
(c)\[\frac{AB}{EF} = \frac{AC}{DE}\]
(d)\[\frac{BC}{DF} = \frac{AB}{EF}\]
In ∆ABC, a line XY parallel to BC cuts AB at X and AC at Y. If BY bisects ∠XYC, then
In a ∆ABC, perpendicular AD from A and BC meets BC at D. If BD = 8 cm, DC = 2 cm and AD = 4 cm, then
