Advertisements
Advertisements
Question
∆ABC is an isosceles triangle in which ∠C = 90. If AC = 6 cm, then AB =
Options
- \[6\sqrt{2} cm\]
6 cm
- \[2\sqrt{6} cm\]
- \[4\sqrt{2} cm\]
Solution
Given: In an isosceles ΔABC, `∠C= 90^o`, AC = 6 cm.
To find: AB
In an isosceles ΔABC, `∠C= 90^o`,.
Therefore, BC = AC = 6 cm
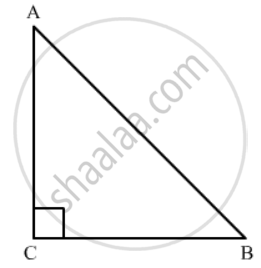
Applying Pythagoras theorem in ΔABC, we get
`AB^2=AC^2+BC^2`
`AB^2=6^2+6^2(AC=BC)`(Side of isosceles triangle)
`AB^2=36+36`
`AB^2=72`
`AB= 6sqrt2 cm`
We got the result as `a`.
APPEARS IN
RELATED QUESTIONS
A girl of height 90 cm is walking away from the base of a lamp-post at a speed of 1.2m/sec. If the lamp is 3.6 m above the ground, find the length of her shadow after 4 seconds.
What values of x will make DE || AB in the given figure?

ABCD is a trapezium having AB || DC. Prove that O, the point of intersection of diagonals, divides the two diagonals in the same ratio. Also prove that
Corresponding sides of two triangles are in the ratio 2 : 3. If the area of the smaller triangle is 48 cm2, determine the area of the larger triangle.
In ∆ABC, ∠C is an obtuse angle. AD ⊥ BC and AB2 = AC2 + 3 BC2. Prove that BC = CD.
In ∆ABC, given that AB = AC and BD ⊥ AC. Prove that BC2 = 2 AC. CD
In ∆ABC, AD is a median. Prove that AB2 + AC2 = 2AD2 + 2DC2.
In a ∆ABC, AD is the bisector of ∠BAC. If AB = 8 cm, BD = 6 cm and DC = 3 cm. Find AC
In the given figure, if PB || CF and DP || EF, then \[\frac{AD}{DE} =\]
In a ∆ABC, ∠A = 90°, AB = 5 cm and AC = 12 cm. If AD ⊥ BC, then AD =
