Advertisements
Advertisements
Question
Corresponding sides of two triangles are in the ratio 2 : 3. If the area of the smaller triangle is 48 cm2, determine the area of the larger triangle.
Solution
The ratio of the areas of two similar triangles is equal to the ratio of the square of any two corresponding sides.
`\text{(Area of triangle)}/\text{(Area of larger triangle)}=\text{(Corresponding side of smaller triangle)}^2/\text{(Corresponding side of larger triangle)}^2`
`\text{(Area of triangle)}/\text{(Area of larger triangle)}= 2^2/3^2`
`48/\text{(Area of larger triangle)}= 4/9`
Area of larger triangle =`(48xx9)/4`
Area of larger triangle = 108
Hence the area of the larger triangle is ` 108 cm^2`
APPEARS IN
RELATED QUESTIONS
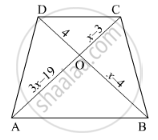
In below figure, AB || CD. If OA = 3x – 19, OB = x – 4, OC = x – 3 and OD = 4, find x.
In the given figure, given that ∆ABC ∼ ∆PQR and quad ABCD ∼ quad PQRS. Determine the value of x, y, z in each case.
In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.

In ∆PQR, M and N are points on sides PQ and PR respectively such that PM = 15 cm and NR = 8 cm. If PQ = 25 cm and PR = 20 cm state whether MN || QR.
State Pythagoras theorem and its converse.
In the given figure, DE || BC in ∆ABC such that BC = 8 cm, AB = 6 cm and DA = 1.5 cm. Find DE.

In triangles ABC and DEF, ∠A = ∠E = 40°, AB : ED = AC : EF and ∠F = 65°, then ∠B =
∆ABC ∼ ∆PQR such that ar(∆ABC) = 4 ar(∆PQR). If BC = 12 cm, then QR =
A vertical stick 20 m long casts a shadow 10 m long on the ground. At the same time, a tower casts a shadow 50 m long on the ground. The height of the tower is
In a ∆ABC, ∠A = 90°, AB = 5 cm and AC = 12 cm. If AD ⊥ BC, then AD =
