Advertisements
Advertisements
Question
In ∆PQR, M and N are points on sides PQ and PR respectively such that PM = 15 cm and NR = 8 cm. If PQ = 25 cm and PR = 20 cm state whether MN || QR.
Solution
Given PM = 15 cm,MQ = 10 cm , NR = 8 cm and PN = 12 cm .
\[\frac{PN}{PR} = \frac{12cm}{20cm} = \frac{3}{5} \left( PN = PR - NR = 20 - 8 = 12cm \right)\]
\[ \therefore \frac{PM}{PQ} = \frac{PN}{PR}\]
So, by the converse of basic proportionality theorem MN || QR.
APPEARS IN
RELATED QUESTIONS
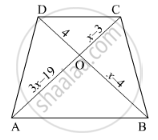
In below figure, AB || CD. If OA = 3x – 19, OB = x – 4, OC = x – 3 and OD = 4, find x.
In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :

In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.
Corresponding sides of two similar triangles are in the ratio 1 : 3. If the area of the smaller triangle in 40 cm2, find the area of the larger triangle.
The diagonals of quadrilateral ABCD intersect at O. Prove that
`[A(∆"ACB")]/[A(∆"ACD")] = "BO"/"DO"`
ABCD is a rectangle. Points M and N are on BD such that AM ⊥ BD and CN ⊥ BD. Prove that BM2 + BN2 = DM2 + DN2.
The areas of two similar triangles are 169 cm2 and 121 cm2 respectively. If the longest side of the larger triangle is 26 cm, what is the length of the longest side of the smaller triangle?
The lengths of the diagonals of a rhombus are 30 cm and 40 cm. Find the side of the rhombus.
Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio.
The areas of two similar triangles are 121 cm2 and 64 cm2 respectively. If the median of the first triangle is 12.1 cm, then the corresponding median of the other triangle is
