Advertisements
Advertisements
Question
In ∆ABC, P and Q are points on sides AB and AC respectively such that PQ || BC. If AP = 3 cm, PB = 5 cm and AC = 8 cm, find AQ.
Solution
In Δ ABC, P and Q are points on sides AB and AC respectively such that `PQ|| BC`
Then we have
`(AP)/(AB)=(AQ)/(AC)`
AP = 3cm ,PB = 5cm ,AC = 8cm and AB = cm
`3/8=(AQ)/8`
`3/cancel8=(AQ)/cancel8`
`3= AQ`
Hence the value of AQ is 3 cm.
APPEARS IN
RELATED QUESTIONS
In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.
In ∆ABC, the bisector of ∠A intersects BC in D. If AB = 18 cm, AC = 15 cm and BC = 22 cm, find BD.
In ∆ABC, ∠ABC = 135°. Prove that AC2 = AB2 + BC2 + 4 ar (∆ABC)
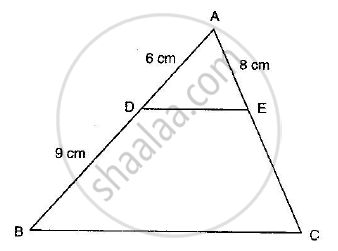
In the adjoining figure, find AC.
State Pythagoras theorem and its converse.
XY is drawn parallel to the base BC of a ∆ABC cutting AB at X and AC at Y. If AB = 4 BX and YC = 2 cm, then AY =
ABCD is a trapezium such that BC || AD and AD = 4 cm. If the diagonals AC and BD intersect at O such that \[\frac{AO}{OC} = \frac{DO}{OB} = \frac{1}{2}\], then BC =
The areas of two similar triangles are 121 cm2 and 64 cm2 respectively. If the median of the first triangle is 12.1 cm, then the corresponding median of the other triangle is
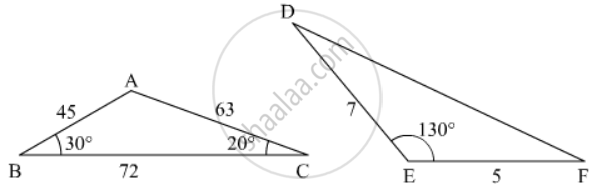
In the given figure the measure of ∠D and ∠F are respectively
∆ABC is a right triangle right-angled at A and AD ⊥ BC. Then, \[\frac{BD}{DC} =\]
