Advertisements
Advertisements
Question
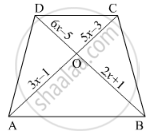
ABCD is a trapezium such that BC || AD and AD = 4 cm. If the diagonals AC and BD intersect at O such that \[\frac{AO}{OC} = \frac{DO}{OB} = \frac{1}{2}\], then BC =
Options
7 cm
8 cm
9 cm
6 cm
Solution
Given: ABCD is a trapezium in which BC||AD and AD = 4 cm
The diagonals AC and BD intersect at O such that `(AO)/(OC)=(DO)/(OB)=1/2`
To find: DC

In ΔAOD and ΔCOB
\[\angle ODA = \angle OBC \left( \text{Alternate angles} \right)\]
\[\angle AOD = \angle BOC \left( \text{Vertically opposite angles} \right)\]
\[So, ∆ AOD~ ∆ COB \left( \text{AAA similarity} \right)\]
\[\text{Now, correponding sides of similar ∆ 's are proportional} . \]
\[\frac{AO}{CO} = \frac{DO}{BO} = \frac{AD}{BC}\]
\[ \Rightarrow \frac{1}{2} = \frac{AD}{BC}\]
\[ \Rightarrow \frac{1}{2} = \frac{4}{BC}\]
\[ \Rightarrow BC = 8 cm\]
Hence the correct answer is `b`
APPEARS IN
RELATED QUESTIONS
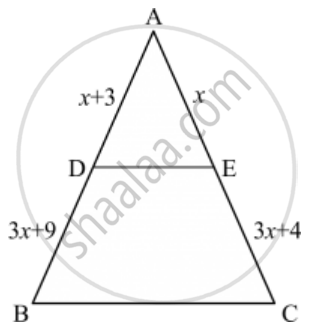
In the below figure, If AB || CD, find the value of x.
In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.

In ∆PQR, M and N are points on sides PQ and PR respectively such that PM = 15 cm and NR = 8 cm. If PQ = 25 cm and PR = 20 cm state whether MN || QR.
In the given figure,

AB || DC prove that
DM × BV = BM ✕ DU
In ∆ABC, AD and BE are altitude. Prove that\[\frac{ar\left( ∆ DEC \right)}{ar\left( ∆ ABC \right)} = \frac{{DC}^2}{{AC}^2}\]
State SAS similarity criterion.
The lengths of the diagonals of a rhombus are 30 cm and 40 cm. Find the side of the rhombus.
If ABC and DEF are similar triangles such that ∠A = 47° and ∠E = 83°, then ∠C =
∆ABC ∼ ∆PQR such that ar(∆ABC) = 4 ar(∆PQR). If BC = 12 cm, then QR =
In the given figure, the value of x for which DE || AB is