Advertisements
Advertisements
Question
In the given figure,

AB || DC prove that
DM × BV = BM ✕ DU
Solution
Since ` ∆DMU ∼ ∆BMV`
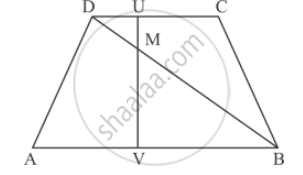
`(DM)/(BM)=(MU)/(MV)=(DU)/(BV)`
`(DM)/(BM)=(DU)/(BV)`
By cross multiplication, we get `DMxxBVxxDUxxBM`
Hence proved that `DMxxBVxxDUxxBM`
APPEARS IN
RELATED QUESTIONS
In the below figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm, such that the segments BD and DC are respectively of lengths 6 cm and 9 cm. If the area of Δ ABC is 54 cm2, then find the lengths of sides AB and AC.

In an isosceles ΔABC, the base AB is produced both the ways to P and Q such that AP × BQ = AC2. Prove that ΔAPC ~ ΔBCQ.
In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.

In ∆ABC, the bisector of ∠A intersects BC in D. If AB = 18 cm, AC = 15 cm and BC = 22 cm, find BD.
In each of the figures given below, an altitude is drawn to the hypotenuse by a right-angled triangle. The length of different line-segment are marked in each figure. Determine x, y, z in each case.
If the altitude of two similar triangles are in the ratio 2 : 3, what is the ratio of their areas?
∆ABC and ∆BDE are two equilateral triangles such that D is the mid-point of BC. The ratio of the areas of triangle ABC and BDE is
If ABC is a right triangle right-angled at B and M, N are the mid-points of AB and BC respectively, then 4(AN2 + CM2) =
∆ABC ∼ ∆PQR such that ar(∆ABC) = 4 ar(∆PQR). If BC = 12 cm, then QR =
If in two triangle ABC and DEF, ∠A = ∠E, ∠B = ∠F, then which of the following is not true?
(a)\[\frac{BC}{DF} = \frac{AC}{DE}\]
(b)\[\frac{AB}{DE} = \frac{BC}{DF}\]
(c)\[\frac{AB}{EF} = \frac{AC}{DE}\]
(d)\[\frac{BC}{DF} = \frac{AB}{EF}\]
