Advertisements
Advertisements
Question
In ∆ABC, the bisector of ∠A intersects BC in D. If AB = 18 cm, AC = 15 cm and BC = 22 cm, find BD.
Solution
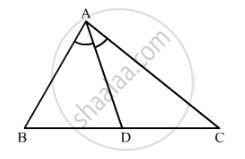
We have to find the value of BD.
Given AB = 18cm ,AC= 15cm and `BC = 22cm`.
In Δ ABC, AD the bisector of `∠ A.`.
`(AB)/(AC)=(BD)/(DC)`
`(AB)/(AC)=(BD)/(BC-BD)`
`18/15=(BD)/(22-BD)`
On cross multiplication, we get
`6(22-BD)=5xxBD`
`132-6BD=5BD`
`132=5BD+6BD`
`132=11BD`
`BD=12cm`
Hence, the value of BD is 12 cm.
APPEARS IN
RELATED QUESTIONS
In below Figure, ΔABC is right angled at C and DE ⊥ AB. Prove that ΔABC ~ ΔADE and Hence find the lengths of AE and DE.

In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :

In the given figure,

AB || DC prove that
(i) ∆DMU ∼ ∆BMV
The areas of two similar triangles are 169 cm2 and 121 cm2 respectively. If the longest side of the larger triangle is 26 cm, what is the length of the longest side of the smaller triangle?
If ABC and DEF are similar triangles such that ∠A = 57° and ∠E = 73°, what is the measure of ∠C?
If ABC and DEF are similar triangles such that ∠A = 47° and ∠E = 83°, then ∠C =
The length of the hypotenuse of an isosceles right triangle whose one side is\[4\sqrt{2} cm\]
A man goes 24 m due west and then 7 m due north. How far is he from the starting point?
In the given figure, if ∠ADE = ∠ABC, then CE =
If ABC is an isosceles triangle and D is a point of BC such that AD ⊥ BC, then
