Advertisements
Advertisements
Question
In the given figure, ∆AMB ∼ ∆CMD; determine MD in terms of x, y and z.
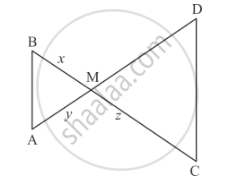
Solution
We are given ∆AMB ∼ ∆CMD
We have to determine the value of MD in terms of x, y and z.
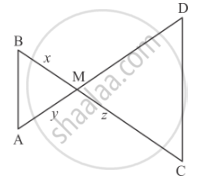
Given `Δ AMB ∼ Δ CMD `
\[\Rightarrow \frac{BM}{MD} = \frac{AM}{CM}\]
\[\frac{x}{MD} = \frac{y}{z}\]
By cross multiplication we get `MD = (xz)/y`
Hence, the value of MD is `(xz)/y`.
APPEARS IN
RELATED QUESTIONS
ABCD is a quadrilateral in which AD = BC. If P, Q, R, S be the mid-points of AB, AC, CD and BD respectively, show that PQRS is a rhombus.
D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AB = 10.8cm, AD = 6.3cm, AC = 9.6cm and EC = 4cm.
What values of x will make DE || AB in the given figure?

In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.

In ∆ABC, if BD ⊥ AC and BC2 = 2 AC . CD, then prove that AB = AC.
If ABC and DEF are similar triangles such that ∠A = 57° and ∠E = 73°, what is the measure of ∠C?
In the given figure, DE || BC in ∆ABC such that BC = 8 cm, AB = 6 cm and DA = 1.5 cm. Find DE.

In an equilateral triangle ABC if AD ⊥ BC, then AD2 =
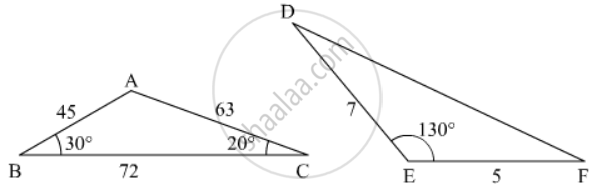
In the given figure the measure of ∠D and ∠F are respectively
∆ABC is such that AB = 3 cm, BC = 2 cm and CA = 2.5 cm. If ∆DEF ∼ ∆ABC and EF = 4 cm, then perimeter of ∆DEF is
