Advertisements
Advertisements
Question
∆ABC is such that AB = 3 cm, BC = 2 cm and CA = 2.5 cm. If ∆DEF ∼ ∆ABC and EF = 4 cm, then perimeter of ∆DEF is
Options
7.5 cm
15 cm
22.5 cm
30 cm
Solution
Given: In ΔABC, AB = 3cm, BC = 2cm, CA = 2.5cm. `ΔDEF ∼ Δ ABC ` and EF = 4cm.
To find: Perimeter of ΔDEF.
We know that if two triangles are similar, then their sides are proportional
Since ΔABC and ΔDEF are similar,
`(AB)/(DE)=(BC)/(EF)=(CA)/(FD)`
`3/(DE)=2/4=2.5/(FD)`
`3/(DE)=2/4`...............(1)
`DE=6cm`
`2/4=2.5/(FD)`
`FD=5cm......................(2)
From (1) and (2), we get
Perimeter of ΔDEF = DE + EF + FD = 6 + 4 +5 = 15 cm
Hence the correct answer is `b`
APPEARS IN
RELATED QUESTIONS
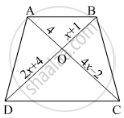
In below figure, If AB || CD, find the value of x.
In below Figure, ΔABC is right angled at C and DE ⊥ AB. Prove that ΔABC ~ ΔADE and Hence find the lengths of AE and DE.

In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :

In the given figure, given that ∆ABC ∼ ∆PQR and quad ABCD ∼ quad PQRS. Determine the value of x, y, z in each case.
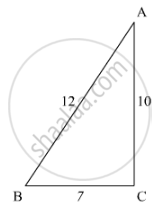
In the adjoining figure, find AC.
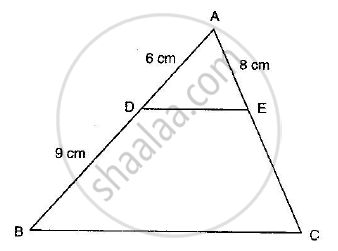
If the altitude of two similar triangles are in the ratio 2 : 3, what is the ratio of their areas?
XY is drawn parallel to the base BC of a ∆ABC cutting AB at X and AC at Y. If AB = 4 BX and YC = 2 cm, then AY =
Two poles of height 6 m and 11 m stand vertically upright on a plane ground. If the distance between their foot is 12 m, the distance between their tops is
In a right triangle ABC right-angled at B, if P and Q are points on the sides AB and AC respectively, then
In the given figure, Δ AHK ∼ Δ ABC. If AK = 8 cm, BC = 3.2 cm and HK = 6.4 cm, then find the length of AC.

