Advertisements
Advertisements
Question
In the given figure, given that ∆ABC ∼ ∆PQR and quad ABCD ∼ quad PQRS. Determine the value of x, y, z in each case.
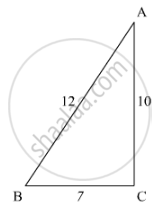
Solution
(i) We have, `Δ ABC ∼ Δ PQR `
So the ratio of the sides of the triangles will be proportional to each other.
`(AB)/(PQ)=(BC)/(QR)=(AC)/(PR)`
Therefore put the values of the known terms in the above equation to get,
`12/9=7/x=10/y`
On solving these simultaneous equations, we get
`x= 21/4`
`y = 30/4`
APPEARS IN
RELATED QUESTIONS
Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using similarity criterion for two triangles, show that `"OA"/"OC"="OB"/"OD"`.
In the given figure, given that ∆ABC ∼ ∆PQR and quad ABCD ∼ quad PQRS. Determine the value of x, y, z in each case.

In ∆ABC, P and Q are points on sides AB and AC respectively such that PQ || BC. If AP = 4 cm, PB = 6 cm and PQ = 3 cm, determine BC.
ABCD is a trapezium having AB || DC. Prove that O, the point of intersection of diagonals, divides the two diagonals in the same ratio. Also prove that
State AAA similarity criterion.
In the given figure, ∆AHK is similar to ∆ABC. If AK = 10 cm, BC = 3.5 cm and HK = 7 cm, find AC.

In an equilateral triangle ABC if AD ⊥ BC, then
In a ∆ABC, ∠A = 90°, AB = 5 cm and AC = 12 cm. If AD ⊥ BC, then AD =
In a ∆ABC, perpendicular AD from A and BC meets BC at D. If BD = 8 cm, DC = 2 cm and AD = 4 cm, then
∆ABC is a right triangle right-angled at A and AD ⊥ BC. Then, \[\frac{BD}{DC} =\]
