Advertisements
Advertisements
प्रश्न
In the given figure, given that ∆ABC ∼ ∆PQR and quad ABCD ∼ quad PQRS. Determine the value of x, y, z in each case.
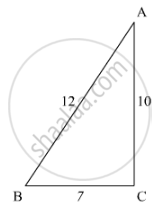
उत्तर
(i) We have, `Δ ABC ∼ Δ PQR `
So the ratio of the sides of the triangles will be proportional to each other.
`(AB)/(PQ)=(BC)/(QR)=(AC)/(PR)`
Therefore put the values of the known terms in the above equation to get,
`12/9=7/x=10/y`
On solving these simultaneous equations, we get
`x= 21/4`
`y = 30/4`
APPEARS IN
संबंधित प्रश्न
ABCD is a quadrilateral in which AD = BC. If P, Q, R, S be the mid-points of AB, AC, CD and BD respectively, show that PQRS is a rhombus.
In a ΔABC, AD is the bisector of ∠A.
If AB = 6.4cm, AC = 8cm and BD = 5.6cm, find DC.
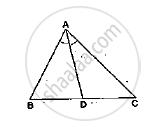
In ∆ABC, D and E are points on sides AB and AC respectively such that AD ✕ EC = AE ✕ DB. Prove that DE || BC.
Nazima is fly fishing in a stream. The tip of her fishing rod is 1.8 m above the surface of the water and the fly at the end of the string rests on the water 3.6 m away and 2.4 m from a point directly under the tip of the road. Assuming that her string (from the tip of her road to the fly) is taut, how much string does she have out (in the given figure)? If she pulls the string at the rate of 5 cm per second, what will the horizontal distance of the fly from her after 12 seconds.

In the given figure, S and T are points on the sides PQ and PR respectively of ∆PQR such that PT = 2 cm, TR = 4 cm and ST is parallel to QR. Find the ratio of the areas of ∆PST and ∆PQR.

XY is drawn parallel to the base BC of a ∆ABC cutting AB at X and AC at Y. If AB = 4 BX and YC = 2 cm, then AY =
Two poles of height 6 m and 11 m stand vertically upright on a plane ground. If the distance between their foot is 12 m, the distance between their tops is
∆ABC ∼ ∆PQR such that ar(∆ABC) = 4 ar(∆PQR). If BC = 12 cm, then QR =
∆ABC is an isosceles triangle in which ∠C = 90. If AC = 6 cm, then AB =
If ∆ABC ∼ ∆DEF such that AB = 9.1 cm and DE = 6.5 cm. If the perimeter of ∆DEF is 25 cm, then the perimeter of ∆ABC is
