Advertisements
Advertisements
प्रश्न
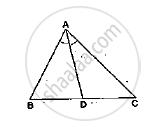
In a ΔABC, AD is the bisector of ∠A.
If AB = 6.4cm, AC = 8cm and BD = 5.6cm, find DC.
उत्तर
It is give that AD bisects ∠A.
Applying angle – bisector theorem in Δ ABC, we get:
`(BD)/(DC)=(AB)/(AC)`
⟹`(5.6)/(DC)=6.4/8`
⟹DC `=(8xx5.6)/6.4=7cm`
APPEARS IN
संबंधित प्रश्न
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC
If AD = 3.6cm, AB = 10cm and AE = 4.5cm, find EC and AC.

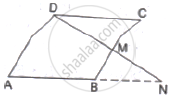
M is a point on the side BC of a parallelogram ABCD. DM when produced meets AB produced at N. Prove that
(1)` (DM)/(MN)=(DC)/(BN)`
(2)` (DN)/(DM)=(AN)/(DC)`
In the given figure, l || m
(i) Name three pairs of similar triangles with proper correspondence; write similarities.
(ii) Prove that

In ∆ABC, if BD ⊥ AC and BC2 = 2 AC . CD, then prove that AB = AC.
The areas of two similar triangles are 169 cm2 and 121 cm2 respectively. If the longest side of the larger triangle is 26 cm, what is the length of the longest side of the smaller triangle?
If ∆ABC and ∆DEF are similar triangles such that AB = 3 cm, BC = 2 cm, CA = 2.5 cm and EF = 4 cm, write the perimeter of ∆DEF.
In the given figure, PQ || BC and AP : PB = 1 : 2. Find\[\frac{area \left( ∆ APQ \right)}{area \left( ∆ ABC \right)}\]

The length of the hypotenuse of an isosceles right triangle whose one side is\[4\sqrt{2} cm\]
∆ABC is an isosceles triangle in which ∠C = 90. If AC = 6 cm, then AB =
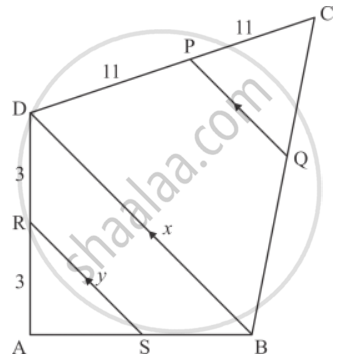
In the given figure, RS || DB || PQ. If CP = PD = 11 cm and DR = RA = 3 cm. Then the values of x and y are respectively.