Advertisements
Advertisements
प्रश्न
The areas of two similar triangles are 169 cm2 and 121 cm2 respectively. If the longest side of the larger triangle is 26 cm, what is the length of the longest side of the smaller triangle?
उत्तर
Let ∆ABC and ΔPQR are similar triangles. The area of triangles is 169cm2 and 121cm2, respectively.
Longest side of the larger triangle is 26cm
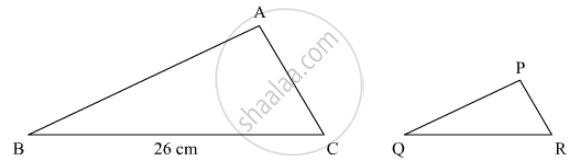
TO FIND: length of longest side of the smaller side.
Suppose longest side of the larger triangle is BC and longest side of the smaller triangle is QR.
We know that the ratio of the areas of two similar triangles is equal to the ratio of the squares of any two corresponding sides.
Hence,
`(ar(Δ ABC))/(ar(Δ PQR))=(BC^2)/(QR^2)`
`169/121=26^2/(QR^2)`
`13/11=26/(QR)`
`QR=(11xx26)/13`
`QR=22`
`QR= 22cm`
APPEARS IN
संबंधित प्रश्न
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC
If AD = 3.6cm, AB = 10cm and AE = 4.5cm, find EC and AC.

In the given figure, DE || BD. Determine AC and AE.

In ∆ABC, P and Q are points on sides AB and AC respectively such that PQ || BC. If AP = 3 cm, PB = 5 cm and AC = 8 cm, find AQ.
In ∆ABC, ∠ABC = 135°. Prove that AC2 = AB2 + BC2 + 4 ar (∆ABC)
State SAS similarity criterion.
In the adjoining figure, DE is parallel to BC and AD = 1 cm, BD = 2 cm. What is the ratio of the area of ∆ABC to the area of ∆ADE?
XY is drawn parallel to the base BC of a ∆ABC cutting AB at X and AC at Y. If AB = 4 BX and YC = 2 cm, then AY =
Two poles of height 6 m and 11 m stand vertically upright on a plane ground. If the distance between their foot is 12 m, the distance between their tops is
In the given figure, if ∠ADE = ∠ABC, then CE =
If ABC is an isosceles triangle and D is a point of BC such that AD ⊥ BC, then
