Advertisements
Advertisements
प्रश्न
If ABC is an isosceles triangle and D is a point of BC such that AD ⊥ BC, then
विकल्प
AB2 − AD2 = BD.DC
AB2 − AD2 = BD2 − DC2
AB2 + AD2 = BD.DC
AB2 + AD2 = BD2 − DC2
उत्तर
Given: ΔABC is an isosceles triangle, D is a point on BC such that `AD ⊥ BC`
We know that in an isosceles triangle the perpendicular from the vertex bisects the base.
∴ BD = DC
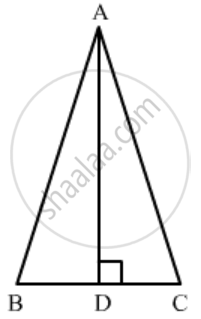
Applying Pythagoras theorem in ΔABD
`AB^2=AD^2+BD^2`
`⇒ AB^2-AD^2=BD^2`
`⇒ AB^2-AD^2=BDxxBD`
Since `BD =DC`
`⇒ AB^2-AD^2=BD xxDC`
Hence correct answer is `a`
APPEARS IN
संबंधित प्रश्न
ABCD is a quadrilateral in which AD = BC. If P, Q, R, S be the mid-points of AB, AC, CD and BD respectively, show that PQRS is a rhombus.
D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AD = 5.7cm, DB = 9.5cm, AE = 4.8cm and EC = 8cm.

D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AB = 10.8cm, AD = 6.3cm, AC = 9.6cm and EC = 4cm.
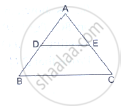
In ∆PQR, M and N are points on sides PQ and PR respectively such that PM = 15 cm and NR = 8 cm. If PQ = 25 cm and PR = 20 cm state whether MN || QR.
In ∆ABC, the bisector of ∠A intersects BC in D. If AB = 18 cm, AC = 15 cm and BC = 22 cm, find BD.
In the adjoining figure, if AD is the bisector of ∠A, what is AC?
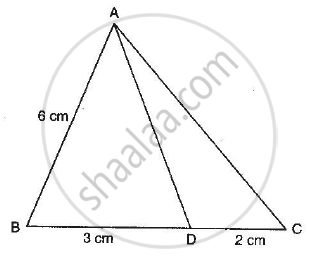
In the given figure, DE || BC and \[AD = \frac{1}{2}BD\]. If BC = 4.5 cm, find DE.
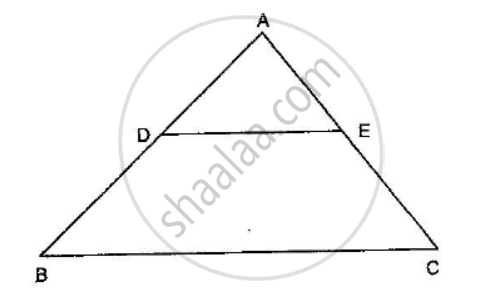
In the given figure, LM = LN = 46°. Express x in terms of a, b and c where a, b, c are lengths of LM, MN and NK respectively.

The areas of two similar triangles are 121 cm2 and 64 cm2 respectively. If the median of the first triangle is 12.1 cm, then the corresponding median of the other triangle is
In an isosceles triangle ABC if AC = BC and AB2 = 2AC2, then ∠C =
