Advertisements
Advertisements
प्रश्न
In the given figure, LM = LN = 46°. Express x in terms of a, b and c where a, b, c are lengths of LM, MN and NK respectively.

उत्तर
Given: In the given figure ∠ LMN = ∠ PNK= `46^o`
TO EXPRESS: x in terms of a, b, c where a, b, and c are the lengths of LM, MN and NK respectively.
Here we can see that. ∠ LMN = ∠ PNK= `46^o` It forms a pair of corresponding angles.
Hence, LM || PN
In
\[\angle LKM = \angle PKN \left( \text{Common} \right)\]
\[ \therefore ∆ LMK~ ∆ PNK \left( \text{AA Similarity} \right)\]
\[\frac{a}{x} = \frac{b + c}{c}\]
\[x = \frac{ac}{b + c}\]
Hence we got the result as \[x = \frac{ac}{b + c}\].
APPEARS IN
संबंधित प्रश्न
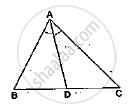
In a ΔABC, AD is the bisector of ∠A.
If AB = 5.6cm, BD = 3.2cm and BC = 6cm, find AC.
In a ΔABC, AD is the bisector of ∠A.
If AB = 5.6cm, AC = 4cm and DC = 3cm, find BC.

In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :

In the given figure, l || m
(i) Name three pairs of similar triangles with proper correspondence; write similarities.
(ii) Prove that

ABCD is a trapezium having AB || DC. Prove that O, the point of intersection of diagonals, divides the two diagonals in the same ratio. Also prove that
A point D is on the side BC of an equilateral triangle ABC such that\[DC = \frac{1}{4}BC\]. Prove that AD2 = 13 CD2.
ABCD is a rectangle. Points M and N are on BD such that AM ⊥ BD and CN ⊥ BD. Prove that BM2 + BN2 = DM2 + DN2.
In the figure given below DE || BC. If AD = 2.4 cm, DB = 3.6 cm, AC = 5 cm. Find AE.
The lengths of the diagonals of a rhombus are 30 cm and 40 cm. Find the side of the rhombus.
In a ∆ABC, ∠A = 90°, AB = 5 cm and AC = 12 cm. If AD ⊥ BC, then AD =
