Advertisements
Advertisements
प्रश्न
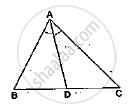
In a ΔABC, AD is the bisector of ∠A.
If AB = 5.6cm, BD = 3.2cm and BC = 6cm, find AC.
उत्तर
It is given that AD bisector ∠𝐴.
Applying angle – bisector theorem in Δ ABC, we get:
`(BD)/(DC)=(AB)/(AC)`
BD = 3.2 cm, BC = 6 cm
Therefore, DC = 6- 3.2 = 2.8 cm
⟹ `3.2/2.8=5.6/(AC)`
⟹ `AC=(5.6xx2.8)/3.2=4.9 cm`
APPEARS IN
संबंधित प्रश्न
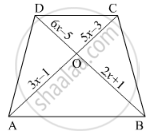
In the below figure, If AB || CD, find the value of x.
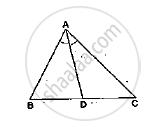
In a ΔABC, AD is the bisector of ∠A.
If AB = 6.4cm, AC = 8cm and BD = 5.6cm, find DC.
A ladder is placed in such a way that its foot is at a distance of 15m from a wall and its top reaches a window 20m above the ground. Find the length of the ladder.
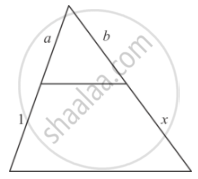
In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :
Corresponding sides of two similar triangles are in the ratio 1 : 3. If the area of the smaller triangle in 40 cm2, find the area of the larger triangle.
Prove that in an equilateral triangle, three times the square of a side is equal to four times the square of its altitudes.
If ∆ABC and ∆DEF are similar triangles such that AB = 3 cm, BC = 2 cm, CA = 2.5 cm and EF = 4 cm, write the perimeter of ∆DEF.
In the given figure, PQ || BC and AP : PB = 1 : 2. Find\[\frac{area \left( ∆ APQ \right)}{area \left( ∆ ABC \right)}\]

In the given figure, S and T are points on the sides PQ and PR respectively of ∆PQR such that PT = 2 cm, TR = 4 cm and ST is parallel to QR. Find the ratio of the areas of ∆PST and ∆PQR.

Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio.
