Advertisements
Advertisements
प्रश्न
Prove that in an equilateral triangle, three times the square of a side is equal to four times the square of its altitudes.
उत्तर
Let ABC be an equilateral triangle and let `AD ⊥ BC`.
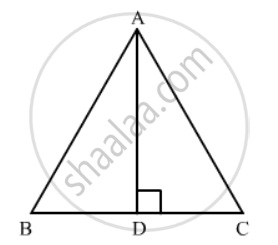
In Δ ADB and Δ ADC we have
`AB=AC`
`∠ B =∠ C`
And ` ∠ ADB = ∠ADC`
So , `BD =DC`
`⇒ BD =DC = 1/2 BC`
Since Δ ADB is a right triangle right-angled at D. So
`AB^2=AD^2+BD^2`
`AB^2=AD^2+(1/2BC)^2`
`AB^2=AD^2+(AB^2)/4`
`3/4 AB^2 =AD^2`
`3AB^2=4AD^2`
Hence proved.
APPEARS IN
संबंधित प्रश्न
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC
If AD = 3.6cm, AB = 10cm and AE = 4.5cm, find EC and AC.

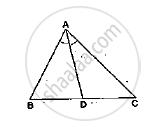
In a ΔABC, AD is the bisector of ∠A.
If AB = 6.4cm, AC = 8cm and BD = 5.6cm, find DC.
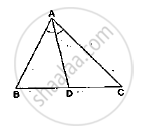
In a ΔABC, AD is the bisector of ∠A.
If AB = 10cm, AC = 14cm and BC = 6cm, find BD and DC.
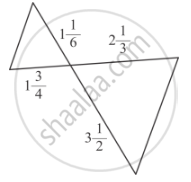
In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.
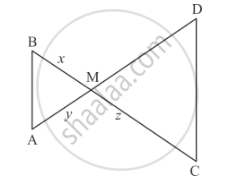
In the given figure, ∆AMB ∼ ∆CMD; determine MD in terms of x, y and z.
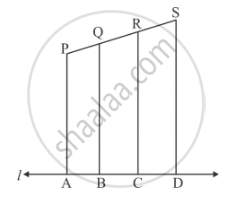
In the given figure, each of PA, QB, RC and SD is perpendicular to l. If AB = 6 cm, BC = 9 cm, CD = 12 cm and PS = 36 cm, then determine PQ, QR and RS.
A point D is on the side BC of an equilateral triangle ABC such that\[DC = \frac{1}{4}BC\]. Prove that AD2 = 13 CD2.
The lengths of the diagonals of a rhombus are 30 cm and 40 cm. Find the side of the rhombus.
A chord of a circle of radius 10 cm subtends a right angle at the centre. The length of the chord (in cm) is
If E is a point on side CA of an equilateral triangle ABC such that BE ⊥ CA, then AB2 + BC2 + CA2 =
