Advertisements
Advertisements
प्रश्न
If E is a point on side CA of an equilateral triangle ABC such that BE ⊥ CA, then AB2 + BC2 + CA2 =
विकल्प
2 BE2
3 BE2
4 BE2
6 BE2
उत्तर
In triangle ABC, E is a point on AC such that `BE ⊥ AC`.
We need to find `AB^2+BC^2+AC^2`.

Since `BE ⊥ AC`, CE = AE =
In triangle ABE, we have
`AB^2 = BE^2+AE^2`
Since AB = BC = AC
Therefore, `AB^2=BC^2=AC^2=BE^2+AE^2`
Since in triangle BE is an altitude, so `BE = (sqrt3)/2 AB`
`BE = (sqrt3)/2 AB`
`(sqrt3)/2 xxAC`
`(sqrt3)/2 xx 2AE= sqrt3AE`
`⇒ AB^2 + BC^2+AC^2= 3BE^2+3((BE)/sqrt3)^2`
`= 3BE^2+BE^2=4BE^2`
Hence option (c) is correct.
APPEARS IN
संबंधित प्रश्न
A vertical stick of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AB = 11.7cm, AC = 11.2cm, BD = 6.5cm and AE = 4.2cm.
The diagonals of quadrilateral ABCD intersect at O. Prove that
`[A(∆"ACB")]/[A(∆"ACD")] = "BO"/"DO"`
In ∆ABC, ray AD bisects ∠A and intersects BC in D. If BC = a, AC = b and AC = c, prove that \[BD = \frac{ac}{b + c}\]
In the given figure, DE || BC and \[AD = \frac{1}{2}BD\]. If BC = 4.5 cm, find DE.
The areas of two similar triangles ∆ABC and ∆DEF are 144 cm2 and 81 cm2 respectively. If the longest side of larger ∆ABC be 36 cm, then the longest side of the smaller triangle ∆DEF is
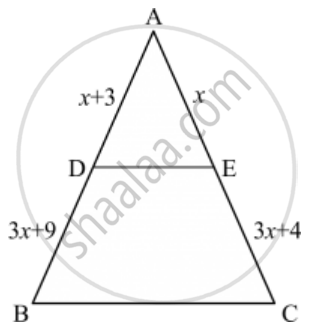
In the given figure, the value of x for which DE || AB is
If ABC is an isosceles triangle and D is a point of BC such that AD ⊥ BC, then
If ∆ABC ∼ ∆DEF such that AB = 9.1 cm and DE = 6.5 cm. If the perimeter of ∆DEF is 25 cm, then the perimeter of ∆ABC is
In an isosceles triangle ABC if AC = BC and AB2 = 2AC2, then ∠C =
