Advertisements
Advertisements
प्रश्न
Prove that in an equilateral triangle, three times the square of a side is equal to four times the square of its altitudes.
उत्तर
Let ABC be an equilateral triangle and let `AD ⊥ BC`.
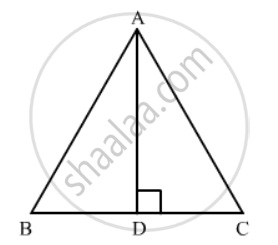
In Δ ADB and Δ ADC we have
`AB=AC`
`∠ B =∠ C`
And ` ∠ ADB = ∠ADC`
So , `BD =DC`
`⇒ BD =DC = 1/2 BC`
Since Δ ADB is a right triangle right-angled at D. So
`AB^2=AD^2+BD^2`
`AB^2=AD^2+(1/2BC)^2`
`AB^2=AD^2+(AB^2)/4`
`3/4 AB^2 =AD^2`
`3AB^2=4AD^2`
Hence proved.
APPEARS IN
संबंधित प्रश्न
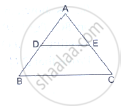
D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AB = 10.8cm, AD = 6.3cm, AC = 9.6cm and EC = 4cm.
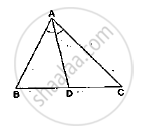
In a ΔABC, AD is the bisector of ∠A.
If AB = 10cm, AC = 14cm and BC = 6cm, find BD and DC.
Corresponding sides of two triangles are in the ratio 2 : 3. If the area of the smaller triangle is 48 cm2, determine the area of the larger triangle.
A point D is on the side BC of an equilateral triangle ABC such that\[DC = \frac{1}{4}BC\]. Prove that AD2 = 13 CD2.
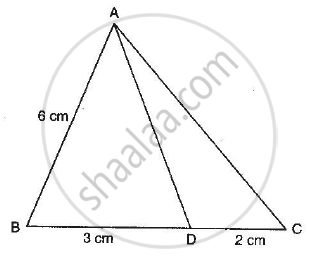
In the adjoining figure, if AD is the bisector of ∠A, what is AC?
If ∆ABC and ∆DEF are similar triangles such that AB = 3 cm, BC = 2 cm, CA = 2.5 cm and EF = 4 cm, write the perimeter of ∆DEF.
In the given figure, LM = LN = 46°. Express x in terms of a, b and c where a, b, c are lengths of LM, MN and NK respectively.

If ABC and DEF are similar triangles such that ∠A = 47° and ∠E = 83°, then ∠C =
In the given figure, if ∠ADE = ∠ABC, then CE =
If E is a point on side CA of an equilateral triangle ABC such that BE ⊥ CA, then AB2 + BC2 + CA2 =
