Advertisements
Advertisements
प्रश्न
In the given figure, LM = LN = 46°. Express x in terms of a, b and c where a, b, c are lengths of LM, MN and NK respectively.

उत्तर
Given: In the given figure ∠ LMN = ∠ PNK= `46^o`
TO EXPRESS: x in terms of a, b, c where a, b, and c are the lengths of LM, MN and NK respectively.
Here we can see that. ∠ LMN = ∠ PNK= `46^o` It forms a pair of corresponding angles.
Hence, LM || PN
In
\[\angle LKM = \angle PKN \left( \text{Common} \right)\]
\[ \therefore ∆ LMK~ ∆ PNK \left( \text{AA Similarity} \right)\]
\[\frac{a}{x} = \frac{b + c}{c}\]
\[x = \frac{ac}{b + c}\]
Hence we got the result as \[x = \frac{ac}{b + c}\].
APPEARS IN
संबंधित प्रश्न
Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using similarity criterion for two triangles, show that `"OA"/"OC"="OB"/"OD"`.
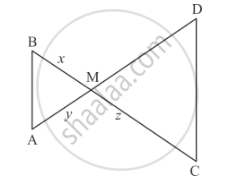
In the given figure, ∆AMB ∼ ∆CMD; determine MD in terms of x, y and z.
In ∆ABC, ray AD bisects ∠A and intersects BC in D. If BC = a, AC = b and AC = c, prove that \[DC = \frac{ab}{b + c}\]
In the adjoining figure, DE is parallel to BC and AD = 1 cm, BD = 2 cm. What is the ratio of the area of ∆ABC to the area of ∆ADE?
If ABC and DEF are similar triangles such that ∠A = 57° and ∠E = 73°, what is the measure of ∠C?
In a ∆ABC, AD is the bisector of ∠BAC. If AB = 8 cm, BD = 6 cm and DC = 3 cm. Find AC
∆ABC ∼ ∆DEF. If BC = 3 cm, EF = 4 cm and ar(∆ABC) = 54 cm2, then ar(∆DEF) =
The areas of two similar triangles are 121 cm2 and 64 cm2 respectively. If the median of the first triangle is 12.1 cm, then the corresponding median of the other triangle is
In ∆ABC, a line XY parallel to BC cuts AB at X and AC at Y. If BY bisects ∠XYC, then
If ∆ABC ∼ ∆DEF such that DE = 3 cm, EF = 2 cm, DF = 2.5 cm, BC = 4 cm, then perimeter of ∆ABC is
