Advertisements
Advertisements
प्रश्न
The areas of two similar triangles are 121 cm2 and 64 cm2 respectively. If the median of the first triangle is 12.1 cm, then the corresponding median of the other triangle is
पर्याय
11 cm
8.8 cm
11.1 cm
8.1 cm
उत्तर
Given: The area of two similar triangles is 121cm2 and 64cm2 respectively. The median of the first triangle is 2.1cm.
To find: Corresponding medians of the other triangle
We know that the ratio of areas of two similar triangles is equal to the ratio of squares of their medians.
`\text{ar(triangle 1)}/\text{ar(triangle 1)}=((\text{median} 1^2)/(\text{median2}^2))^2`
`121/64=((12.1)/\text{median2})^2`
Taking square root on both side, we get
\[ \Rightarrow median2 = 8 . 8 cm\]
Hence the correct answer is `b`.
APPEARS IN
संबंधित प्रश्न
In below figure, If AB || CD, find the value of x.
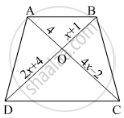
Corresponding sides of two triangles are in the ratio 2 : 3. If the area of the smaller triangle is 48 cm2, determine the area of the larger triangle.
In ∆ABC, ray AD bisects ∠A and intersects BC in D. If BC = a, AC = b and AC = c, prove that \[BD = \frac{ac}{b + c}\]
In a quadrilateral ABCD, ∠B = 90°. If AD2 = AB2 + BC2 + CD2 then prove that ∠ACD = 90°.
If in two triangles ABC and DEF, \[\frac{AB}{DE} = \frac{BC}{FE} = \frac{CA}{FD}\], then
The length of the hypotenuse of an isosceles right triangle whose one side is\[4\sqrt{2} cm\]
A vertical stick 20 m long casts a shadow 10 m long on the ground. At the same time, a tower casts a shadow 50 m long on the ground. The height of the tower is
Two isosceles triangles have equal angles and their areas are in the ratio 16 : 25. The ratio of their corresponding heights is
In a ∆ABC, perpendicular AD from A and BC meets BC at D. If BD = 8 cm, DC = 2 cm and AD = 4 cm, then
If ∆ABC ∼ ∆DEF such that DE = 3 cm, EF = 2 cm, DF = 2.5 cm, BC = 4 cm, then perimeter of ∆ABC is
