Advertisements
Advertisements
प्रश्न
A vertical stick 20 m long casts a shadow 10 m long on the ground. At the same time, a tower casts a shadow 50 m long on the ground. The height of the tower is
पर्याय
100 m
120 m
25 m
200 m
उत्तर
Given: Vertical stick 20m long casts a shadow 10m long on the ground. At the same time a tower casts the shadow 50 m long on the ground.
To determine: Height of the tower
Let AB be the vertical stick and AC be its shadow. Also, let DE be the vertical tower and DF be its shadow.
Join BC and EF.
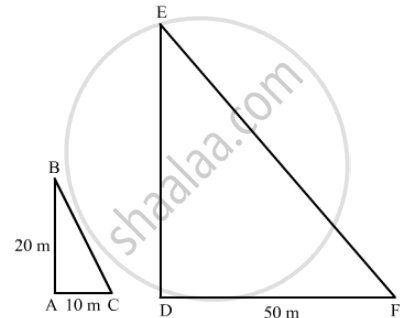
In ΔABC and ΔDEF, we have
`∠A=∠D=90^o`
`∠C=∠F`
`Δ ABC ∼ Δ DEF`
We know that in any two similar triangles, the corresponding sides are proportional. Hence,
`(AB)/(DE)=(AC)/(DF)`
`20/(DE)=10/50`
`DE=100m`
Hence the correct answer is option `a`.
APPEARS IN
संबंधित प्रश्न
In the below figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm, such that the segments BD and DC are respectively of lengths 6 cm and 9 cm. If the area of Δ ABC is 54 cm2, then find the lengths of sides AB and AC.

A girl of height 90 cm is walking away from the base of a lamp-post at a speed of 1.2m/sec. If the lamp is 3.6 m above the ground, find the length of her shadow after 4 seconds.
In ∆ABC, points P and Q are on CA and CB, respectively such that CA = 16 cm, CP = 10 cm, CB = 30 cm and CQ = 25 cm. Is PQ || AB?
In the given figure, l || m
(i) Name three pairs of similar triangles with proper correspondence; write similarities.
(ii) Prove that

In ∆ABC, AD and BE are altitude. Prove that\[\frac{ar\left( ∆ DEC \right)}{ar\left( ∆ ABC \right)} = \frac{{DC}^2}{{AC}^2}\]
There is a staircase as shown in the given figure, connecting points A and B. Measurements of steps are marked in the figure. Find the straight line distance between A and B.

In ∆ABC, if BD ⊥ AC and BC2 = 2 AC . CD, then prove that AB = AC.
In ∆ABC, AD is a median. Prove that AB2 + AC2 = 2AD2 + 2DC2.
A man goes 24 m due west and then 7 m due north. How far is he from the starting point?
∆ABC is such that AB = 3cm, BC = 2cm, CA = 2.5cm. If ∆ABC ~ ∆DEF and EF = 4cm, then perimeter of ∆DEF is ______.
